
| 给定下列命题:其中真命题的个数是( ) (1)若k>0,则方程x2+2x-k=0有实数根; (2)“若a>b,则a+c>b+c”的否命题; (3)“矩形的对角线相等”的逆命题; (4)“若xy=0,则x,y中至少有一个为0”的逆否命题.
|
科目:高中数学 来源:2011-2012学年福建省厦门一中高二(上)期中数学试卷(理科)(解析版) 题型:选择题
科目:高中数学 来源: 题型:
科目:高中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
科目:高中数学 来源: 题型:
科目:高中数学 来源:不详 题型:单选题
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
科目:高中数学 来源:《1.1 命题及其关系》2013年同步练习(解析版) 题型:选择题
科目:高中数学 来源:2012-2013学年北京市石景山区高三(上)期末数学试卷(理科)(解析版) 题型:填空题
 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=x-{x}的四个命题:
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=x-{x}的四个命题: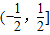 ;
; 上是增函数.
上是增函数.科目:高中数学 来源: 题型:填空题
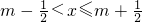 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题: ];
]; (k∈Z)对称;
(k∈Z)对称;科目:高中数学 来源: 题型:解答题
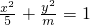 恒有公共点,实数m的取值范围是m≥1
恒有公共点,实数m的取值范围是m≥1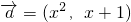 ,
,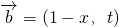 ,若函数f(x)=
,若函数f(x)=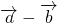 在区间上是增函数,则实数t的取值范围是(5,+∞);
在区间上是增函数,则实数t的取值范围是(5,+∞);科目:高中数学 来源:2010-2011学年四川省成都九中高三(下)3月月考数学试卷(文科)(解析版) 题型:解答题
 恒有公共点,实数m的取值范围是m≥1
恒有公共点,实数m的取值范围是m≥1 ,
, ,若函数f(x)=
,若函数f(x)= 在区间上是增函数,则实数t的取值范围是(5,+∞);
在区间上是增函数,则实数t的取值范围是(5,+∞);湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com