| 已知等比数列{an}的公比q>1,且a2a4=16,a2+a4=10,那么S6=( ) |
相关习题
科目:高中数学
来源:
题型:
已知等比数列{a
n}的公比q>1,且a
1与a
4的一等比中项为
4,a
2与a
3的等差中项为6.
(1)求数列{a
n}的通项公式;
(2)设b
n=log
2a
n,求数列{a
n•b
n}的前n项和T
n;
(3)设S
n为数列{a
n}的前n项和,c
n=S
n+3+(-1)
n+1a
n2(n∈N
*),请比较c
n与c
n+1的大小,并加以说明.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知等比数列{a
n}的公比q>1,且a
1与a
4的一等比中项为
4,a
2与a
3的等差中项为6.
(I)求数列{a
n}的通项公式;
(Ⅱ)设S
n为数列{a
n}的前n项和,b
n=S
n+3+(-1)
n+1a
n2(n∈N
*),请比较b
n与b
n+1的大小;
(Ⅲ)数列{a
n}中是否存在三项,按原顺序成等差数列?若存在,则求出这三项;若不存在,则加以证明.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知等比数列{an}的公比q>1,且a2a4=16,a2+a4=10,那么S6=( )
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知等比数列{an}的公比q>1,且a1与a4的一等比中项为 ,a2与a3的等差中项为6.
,a2与a3的等差中项为6.
(1)求数列{an}的通项公式;
(2)设bn=log2an,求数列{an•bn}的前n项和Tn;
(3)设Sn为数列{an}的前n项和,cn=Sn+3+(-1)n+1an2(n∈N*),请比较cn与cn+1的大小,并加以说明.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知等比数列{a
n}的公比q>1,且a
2a
4=16,a
2+a
4=10,那么S
6=( )
查看答案和解析>>
科目:高中数学
来源:2008-2009学年北京市海淀区高一(下)期中数学试卷(必修5)(解析版)
题型:选择题
已知等比数列{an}的公比q>1,且a2a4=16,a2+a4=10,那么S6=( )
A.64
B.63
C.32
D.31
查看答案和解析>>
科目:高中数学
来源:2010年-2011学安徽省宿州市埇桥区灵璧中学高三第五次月考数学试卷(文科)(解析版)
题型:解答题
已知等比数列{a
n}的公比q>1,且a
1与a
4的一等比中项为
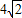
,a
2与a
3的等差中项为6.
(1)求数列{a
n}的通项公式;
(2)设b
n=log
2a
n,求数列{a
n•b
n}的前n项和T
n;
(3)设S
n为数列{a
n}的前n项和,c
n=S
n+3+(-1)
n+1a
n2(n∈N
*),请比较c
n与c
n+1的大小,并加以说明.
查看答案和解析>>
科目:高中数学
来源:2011年广东省深圳市第二高级中学高考数学模拟试卷2(文科)(解析版)
题型:解答题
已知等比数列{a
n}的公比q>1,且a
1与a
4的一等比中项为

,a
2与a
3的等差中项为6.
(I)求数列{a
n}的通项公式;
(Ⅱ)设S
n为数列{a
n}的前n项和,b
n=S
n+3+(-1)
n+1a
n2(n∈N
*),请比较b
n与b
n+1的大小;
(Ⅲ)数列{a
n}中是否存在三项,按原顺序成等差数列?若存在,则求出这三项;若不存在,则加以证明.
查看答案和解析>>
科目:高中数学
来源:2009年广东省深圳市高考数学二模试卷(文科)(解析版)
题型:解答题
已知等比数列{a
n}的公比q>1,且a
1与a
4的一等比中项为

,a
2与a
3的等差中项为6.
(I)求数列{a
n}的通项公式;
(Ⅱ)设S
n为数列{a
n}的前n项和,b
n=S
n+3+(-1)
n+1a
n2(n∈N
*),请比较b
n与b
n+1的大小;
(Ⅲ)数列{a
n}中是否存在三项,按原顺序成等差数列?若存在,则求出这三项;若不存在,则加以证明.
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知等比数列{an}的公比q>1,且a2a4=16,a2+a4=10,那么S6=
- A.
64
- B.
63
- C.
32
- D.
31
查看答案和解析>>

 ,a2与a3的等差中项为6.
,a2与a3的等差中项为6.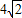 ,a2与a3的等差中项为6.
,a2与a3的等差中项为6. ,a2与a3的等差中项为6.
,a2与a3的等差中项为6. ,a2与a3的等差中项为6.
,a2与a3的等差中项为6.