
下列说法中不正确的是( )
|
科目:初中数学 来源:不详 题型:单选题
| A.所有的有理数都能用数轴上的点表示 |
| B.有理数分为正数和负数 |
| C.符号不同的两个数互为相反数 |
| D.两数相加和一定大于任何一个加数 |
科目:初中数学 来源: 题型:
科目:初中数学 来源:不详 题型:单选题
| A.和数轴上一一对应的数是有理数 |
| B.数轴上的点可以表示所有的实数 |
| C.带根号的数都是无理数 |
| D.不带根号的数都是无理数 |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源:不详 题型:单选题
| A.所有的有理数都可以用数轴上的点表示 |
| B.数轴上的原点表示0 |
| C.在数轴上表示-3的点与表示+1的点的距离是2个单位长度 |
| D.数轴上表示-4的点在原点的左边且距离原点4个单位长度 |
科目:初中数学 来源:不详 题型:单选题
| A.符号不同的两个数互为相反数 |
| B.两个有理数和一定大于每一个加数 |
| C.有理数分为正数和负数 |
| D.所有的有理数都能用数轴上的点来表示 |
科目:初中数学 来源:2012年山东省青岛市李沧区中考数学一模试卷(解析版) 题型:解答题
 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?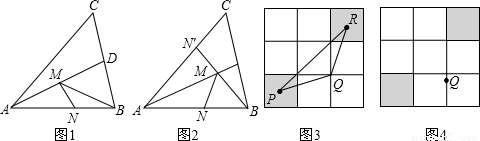
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com