△ABC的顶点坐标为(-2,5),若将△ABC沿x轴平移5个单位,则A点坐标变为( )| A.(3,5) | B.(3,0)或(-7,0) | | C.(3,5)或(-7,5) | D.(-2,0)或(-2,10) |
|
相关习题
科目:初中数学
来源:第34章《二次函数》中考题集(36):34.4 二次函数的应用(解析版)
题型:解答题
如图,Rt△ABC的顶点坐标分别为A(0,

),B(
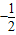
,

),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,

),以点D为顶点y轴为对称轴的抛物线过点B.
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学
来源:第6章《二次函数》中考题集(36):6.4 二次函数的应用(解析版)
题型:解答题
如图,Rt△ABC的顶点坐标分别为A(0,
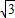
),B(

,
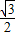
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
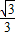
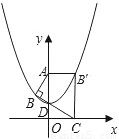
),以点D为顶点y轴为对称轴的抛物线过点B.
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学
来源:第27章《二次函数》中考题集(35):27.3 实践与探索(解析版)
题型:解答题
如图,Rt△ABC的顶点坐标分别为A(0,
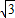
),B(
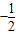
,
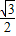
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
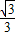
),以点D为顶点y轴为对称轴的抛物线过点B.
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学
来源:第26章《二次函数》中考题集(33):26.3 实际问题与二次函数(解析版)
题型:解答题
如图,Rt△ABC的顶点坐标分别为A(0,
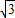
),B(
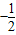
,
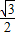
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
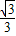
),以点D为顶点y轴为对称轴的抛物线过点B.
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(37):2.8 二次函数的应用(解析版)
题型:解答题
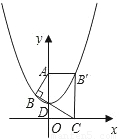
如图,Rt△ABC的顶点坐标分别为A(0,

),B(

,

),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,

),以点D为顶点y轴为对称轴的抛物线过点B.
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学
来源:第20章《二次函数和反比例函数》中考题集(33):20.5 二次函数的一些应用(解析版)
题型:解答题
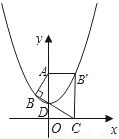
如图,Rt△ABC的顶点坐标分别为A(0,

),B(
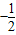
,
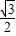
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,

),以点D为顶点y轴为对称轴的抛物线过点B.
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(33):2.4 二次函数的应用(解析版)
题型:解答题
如图,Rt△ABC的顶点坐标分别为A(0,

),B(

,

),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,

),以点D为顶点y轴为对称轴的抛物线过点B.
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学
来源:第23章《二次函数与反比例函数》中考题集(33):23.5 二次函数的应用(解析版)
题型:解答题
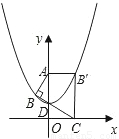
如图,Rt△ABC的顶点坐标分别为A(0,

),B(

,

),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,

),以点D为顶点y轴为对称轴的抛物线过点B.
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学
来源:
题型:
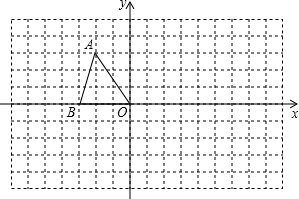
如图将△ABC沿x轴的正方向平移4单位得到△A′B′O′,再绕O′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(-2,3),B点坐标为(-3,0);
①在图中画△A′B′O′和△A″B″O″;
②直接写出A′和A″点的坐标;
③△ABO的顶点A在变换过程中所经过的路径长为多少?
查看答案和解析>>

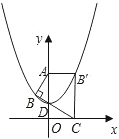 如图,Rt△ABC的顶点坐标分别为A(0,
如图,Rt△ABC的顶点坐标分别为A(0, ),B(
),B( ,
, ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0, ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B. ),B(
),B(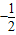 ,
, ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0, ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
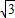 ),B(
),B( ,
,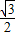 ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,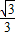 ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
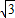 ),B(
),B(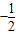 ,
,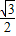 ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,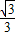 ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
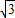 ),B(
),B(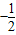 ,
,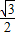 ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,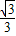 ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
 ),B(
),B( ,
, ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0, ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
 ),B(
),B(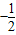 ,
,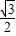 ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0, ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
 ),B(
),B( ,
, ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0, ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
 ),B(
),B( ,
, ),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,
),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0, ),以点D为顶点y轴为对称轴的抛物线过点B.
),以点D为顶点y轴为对称轴的抛物线过点B.
 如图将△ABC沿x轴的正方向平移4单位得到△A′B′O′,再绕O′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(-2,3),B点坐标为(-3,0);
如图将△ABC沿x轴的正方向平移4单位得到△A′B′O′,再绕O′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(-2,3),B点坐标为(-3,0);