若sin2x<cos2x,则x的取值范围是( )| A.{x|2kπ-π<x<2kπ+,k∈Z} | | B.{x|2kπ+<x<2kπ+π,k∈Z} | | C.{x|kπ-<x<kπ+,k∈Z} | | D.{x|kπ+<x<kπ+π,k∈Z} |
|
相关习题
科目:高中数学
来源:2005-2006学年浙江省杭州四中(下沙校区)高一(下)期中数学试卷(解析版)
题型:选择题
若sin
2x<cos
2x,则x的取值范围是( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:
题型:
若sin2x<cos2x,则x的取值范围是( )
| A、{x|2kπ-π<x<2kπ+,k∈Z} |
| B、{x|2kπ+<x<2kπ+π,k∈Z} |
| C、{x|kπ-<x<kπ+,k∈Z} |
| D、{x|kπ+<x<kπ+π,k∈Z} |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若sin
2x<cos
2x,则x的取值范围是( )
| A.{x|2kπ-π<x<2kπ+,k∈Z} |
| B.{x|2kπ+<x<2kπ+π,k∈Z} |
| C.{x|kπ-<x<kπ+,k∈Z} |
| D.{x|kπ+<x<kπ+π,k∈Z} |
查看答案和解析>>
科目:高中数学
来源:2011年广东省高考数学第三轮复习精编模拟试卷07(理科)(解析版)
题型:选择题
若sin
2x>cos
2x,则x的取值范围是( )
A.{x|2kπ-

<x<2kπ+

,k∈Z}
B.{x|2kπ+

<x<2kπ+

,k∈Z}
C.{x|kπ-

<x<kπ+

,k∈Z}
D.{x|kπ+

<x<kπ+
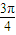
,k∈Z}
查看答案和解析>>
科目:高中数学
来源:
题型:
若sin2x>cos2x,则x的取值范围是( )
| A、{x|2kπ-π<x<2kπ+π,k∈Z} |
| B、{x|2kπ+π<x<2kπ+π,k∈Z} |
| C、{x|kπ-π<x<kπ+π,k∈Z} |
| D、{x|kπ+π<x<kπ+π,k∈Z} |
查看答案和解析>>
科目:高中数学
来源:
题型:
若sin2x>cos2x,则x的取值范围是( )
| A、{x|2kπ-<x<2kπ+,k∈Z} |
| B、{x|2kπ+<x<2kπ+,k∈Z} |
| C、{x|kπ-<x<kπ+,k∈Z} |
| D、{x|kπ+<x<kπ+,k∈Z} |
查看答案和解析>>
科目:高中数学
来源:
题型:
若sin2x>cos2x,则x的取值范围是( )
| A、{x|-+2kπ<x<+2kπ,k∈Z} |
| B、{x|+2kπ<x<+2kπ,k∈Z} |
| C、{x|-+kπ<x<+kπ,k∈Z} |
| D、{x|+kπ<x<+kπ,k∈Z} |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若sin
2x>cos
2x,则x的取值范围是( )
| A.{x|-+2kπ<x<+2kπ,k∈Z} |
| B.{x|+2kπ<x<+2kπ,k∈Z} |
| C.{x|-+kπ<x<+kπ,k∈Z} |
| D.{x|+kπ<x<+kπ,k∈Z} |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若sin
2x>cos
2x,则x的取值范围是( )
| A.{x|2kπ-π<x<2kπ+π,k∈Z} |
| B.{x|2kπ+π<x<2kπ+π,k∈Z} |
| C.{x|kπ-π<x<kπ+π,k∈Z} |
| D.{x|kπ+π<x<kπ+π,k∈Z} |
查看答案和解析>>
科目:高中数学
来源:2011年广东省广州市仲元中学高三数学专题训练:三角函数(解析版)
题型:选择题
若在x∈[0,

]内有两个不同的实数值满足等式cos2x+

sin2x=k+1,则k的取值范围是( )

A.-2≤k≤1
B.-2≤k<1
C.0≤k≤1
D.0≤k<1
查看答案和解析>>





 <x<2kπ+
<x<2kπ+ ,k∈Z}
,k∈Z} <x<2kπ+
<x<2kπ+ ,k∈Z}
,k∈Z} <x<kπ+
<x<kπ+ ,k∈Z}
,k∈Z} <x<kπ+
<x<kπ+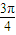 ,k∈Z}
,k∈Z} ]内有两个不同的实数值满足等式cos2x+
]内有两个不同的实数值满足等式cos2x+ sin2x=k+1,则k的取值范围是( )
sin2x=k+1,则k的取值范围是( )