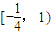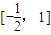定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s2-2s）≤-f（2t-t2）．则当1≤s≤4时，的取值范围是（ ）| A．[-，1) | B．[-，1) | C．[-，1] | D．[-，1] |
|
相关习题
科目：高中数学
来源：
题型：
定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s
2-2s）≤-f（2t-t
2）．则当1≤s≤4时，
的取值范围是（ ）
| A、[-，1) |
| B、[-，1) |
| C、[-，1] |
| D、[-，1] |
查看答案和解析>>
科目：高中数学
来源：
题型：
定义在R上的函数y=f（x）是减函数，y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s
2-2s）≤-f（2t-t
2），则当
1≤s≤4时，的取值范围是
．
查看答案和解析>>
科目：高中数学
来源：
题型：
定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若实数s满足不等式f（s
2-2s）+f（2-s）≤0，则s的取值范围是
（-∞，1]∪[2，+∞）
（-∞，1]∪[2，+∞）
．
查看答案和解析>>
科目：高中数学
来源：
题型：
定义在R上的函数y=f（x）是减函数，且对任意的a∈R，都有f（-a）+f（a）=0，若x，y满足不等式f（x2-2x）+f（2y-y2）≤0，则当1≤x≤4时，2x-y的最大值为（ ）
查看答案和解析>>
科目：高中数学
来源：双流县三模
题型：单选题
定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s
2-2s）≤-f（2t-t
2）．则当1≤s≤4时，
的取值范围是（ ）
| A．[-，1) | B．[-，1) | C．[-，1] | D．[-，1] |
查看答案和解析>>
科目：高中数学
来源：2012-2013学年北京市十一学校高三（上）暑期检测数学试卷3（理科）（解析版）
题型：选择题
定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s
2-2s）≤-f（2t-t
2）．则当1≤s≤4时，
的取值范围是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学
来源：2012-2013学年北京市十一学校高三（上）暑期检测数学试卷3（理科）（解析版）
题型：选择题
定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s
2-2s）≤-f（2t-t
2）．则当1≤s≤4时，
的取值范围是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学
来源：2010-2011学年重庆八中高三（下）第七次月考数学试卷（理科）（解析版）
题型：选择题
定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s
2-2s）≤-f（2t-t
2）．则当1≤s≤4时，
的取值范围是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学
来源：2010-2011学年湖北省邵阳市洞口一中高三（上）第三次月考数学试卷（理科）（解析版）
题型：选择题
定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s
2-2s）≤-f（2t-t
2）．则当1≤s≤4时，
的取值范围是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学
来源：2011-2012学年四川省南充高中高三第六次月考数学试卷（文科）（解析版）
题型：选择题
定义在R上的函数y=f（x）是减函数，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s
2-2s）≤-f（2t-t
2）．则当1≤s≤4时，
的取值范围是（ ）
A．
B．
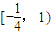
C．
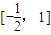
D．
查看答案和解析>>
