练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    三条直线l1：x-y=0，l2：x+y-2=0，l3：5x-ky-15=0构成一个三角形，则k的取值范围是（　　）
    A．k∈RB．k∈R且k≠±1，k≠0
    C．k∈R且k≠±5，k≠-10D．k∈R且k≠±5，k≠1
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    三条直线l1：x-y=0，l2：x+y-2=0，l3：5x-ky-15=0构成一个三角形，则k的取值范围是（　　）
    A、k∈RB、k∈R且k≠±1，k≠0C、k∈R且k≠±5，k≠-10D、k∈R且k≠±5，k≠1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    三条直线l1：x-y=0，l2：x+y-2=0：，l3：5x-ky-15=0，不构成一个三角形，则实数k的所有取值之和为
    -10
    -10
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    三条直线l1：x-y=0，l2：x+y-2=0，l3：5x-ky-15=0构成一个三角形，则k的取值范围是


    1. A.
      k∈R
    2. B.
      k∈R且k≠±1，k≠0
    3. C.
      k∈R且k≠±5，k≠-10
    4. D.
      k∈R且k≠±5，k≠1

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    三条直线l1：x-y=0，l2：x+y-2=0，l3：5x-ky-15=0构成一个三角形，则k的取值范围是（　　）
    A．k∈RB．k∈R且k≠±1，k≠0
    C．k∈R且k≠±5，k≠-10D．k∈R且k≠±5，k≠1

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河北省唐山一中高二（上）期中数学试卷（解析版） 题型：填空题

    三条直线l1：x-y=0，l2：x+y-2=0：，l3：5x-ky-15=0，不构成一个三角形，则实数k的所有取值之和为    ．

    查看答案和解析>>

    科目：高中数学 来源：《3.2 两条直线的位置关系》2013年高考数学优化训练（解析版） 题型：选择题

    三条直线l1：x-y=0，l2：x+y-2=0，l3：5x-ky-15=0构成一个三角形，则k的取值范围是（ ）
    A．k∈R
    B．k∈R且k≠±1，k≠0
    C．k∈R且k≠±5，k≠-10
    D．k∈R且k≠±5，k≠1

    查看答案和解析>>

    科目：高中数学 来源：2011年高三数学第一轮复习巩固与练习：两直线的位置关系（解析版） 题型：选择题

    三条直线l1：x-y=0，l2：x+y-2=0，l3：5x-ky-15=0构成一个三角形，则k的取值范围是（ ）
    A．k∈R
    B．k∈R且k≠±1，k≠0
    C．k∈R且k≠±5，k≠-10
    D．k∈R且k≠±5，k≠1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    三条直线l1：x-y=0，l2：x+y-2=0：，l3：5x-ky-15=0，不构成一个三角形，则实数k的所有取值之和为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l1：x-y=0，l2：x+y=0，点P是线性约束条件
    x-y≥0
    x+y≥0
    所表示区域内一动点，PM⊥l1，PN⊥l2，垂足分别为M、N，且S△OMN=
    1
    2
    （O为坐标原点）．
    （Ⅰ）求动点P的轨迹方程；
    （Ⅱ）是否存在过点（2，0）的直线l与（Ⅰ）中轨迹交于点A、B，线段AB的垂直平分线交y轴于Q点，且使得△ABQ是等边三角形．若存在，求出直线l的方程，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

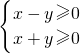    已知直线l1：x-y=0，l2：x+y=0，点P是线性约束条件数学公式所表示区域内一动点，PM⊥l1，PN⊥l2，垂足分别为M、N，且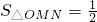数学公式（O为坐标原点）．
    （Ⅰ）求动点P的轨迹方程；
    （Ⅱ）是否存在过点（2，0）的直线l与（Ⅰ）中轨迹交于点A、B，线段AB的垂直平分线交y轴于Q点，且使得△ABQ是等边三角形．若存在，求出直线l的方程，若不存在，说明理由．

    查看答案和解析>>


    同步练习册答案