| 函数f(x)=Asinωx(ω>0),对任意x有f(x-)=f(x+),且f(-)=-a,那么f()等于( ) |
相关习题
科目:高中数学
来源:
题型:
函数f(x)=Asinωx(ω>0),对任意x有
f(x-)=f(x+),且
f(-)=-a,那么
f()等于( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数f(x)=Asinωx(ω>0),对任意x有
f(x-)=f(x+),且
f(-)=-a,那么
f()等于( )
查看答案和解析>>
科目:高中数学
来源:2010年广东省高考数学冲刺预测试卷04(理科)(解析版)
题型:选择题
函数f(x)=Asinωx(ω>0),对任意x有

,且

,那么
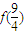
等于( )
A.a
B.

a
C.

a
D.-a
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
函数f(x)=Asinωx(ω>0),对任意x有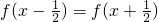 ,且
,且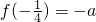 ,那么
,那么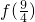 等于
等于
- A.
a
- B.
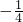
a
- C.

a
- D.
-a
查看答案和解析>>
科目:高中数学
来源:安徽模拟
题型:单选题
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1和x=-1处分别取得最大值和最小值,且对于任意
x1,x2∈[-1,1],x1≠x2,都有>0,则( )
| A.函数y=f(x+1)一定是周期为4的偶函数 |
| B.函数y=f(x+1)一定是周期为2的奇函数 |
| C.函数y=f(x+1)一定是周期为4的奇函数 |
| D.函数y=f(x+1)一定是周期为2的偶函数 |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省滨州市滨城一中高三(上)质检数学试卷(理科)(解析版)
题型:选择题
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1和x=-1处分别取得最大值和最小值,且对于任意

,则( )
A.函数y=f(x+1)一定是周期为4的偶函数
B.函数y=f(x+1)一定是周期为2的奇函数
C.函数y=f(x+1)一定是周期为4的奇函数
D.函数y=f(x+1)一定是周期为2的偶函数
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江西省上饶市上饶县中学高三(上)第一次月考数学试卷(文科)(特、零)(解析版)
题型:选择题
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1和x=-1处分别取得最大值和最小值,且对于任意
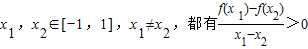
,则( )
A.函数y=f(x+1)一定是周期为4的偶函数
B.函数y=f(x+1)一定是周期为2的奇函数
C.函数y=f(x+1)一定是周期为4的奇函数
D.函数y=f(x+1)一定是周期为2的偶函数
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省滨州市滨城一中高三(上)质检数学试卷(理科)(解析版)
题型:选择题
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1和x=-1处分别取得最大值和最小值,且对于任意

,则( )
A.函数y=f(x+1)一定是周期为4的偶函数
B.函数y=f(x+1)一定是周期为2的奇函数
C.函数y=f(x+1)一定是周期为4的奇函数
D.函数y=f(x+1)一定是周期为2的偶函数
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省江南十校新高三摸底联考数学试卷 (理科)(解析版)
题型:选择题
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1和x=-1处分别取得最大值和最小值,且对于任意

,则( )
A.函数y=f(x+1)一定是周期为4的偶函数
B.函数y=f(x+1)一定是周期为2的奇函数
C.函数y=f(x+1)一定是周期为4的奇函数
D.函数y=f(x+1)一定是周期为2的偶函数
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1和x=-1处分别取得最大值和最小值,且对于任意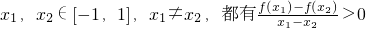 ,则
,则
- A.
函数y=f(x+1)一定是周期为4的偶函数
- B.
函数y=f(x+1)一定是周期为2的奇函数
- C.
函数y=f(x+1)一定是周期为4的奇函数
- D.
函数y=f(x+1)一定是周期为2的偶函数
查看答案和解析>>

 ,且
,且 ,那么
,那么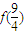 等于( )
等于( ) a
a a
a ,则( )
,则( )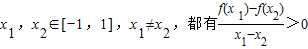 ,则( )
,则( ) ,则( )
,则( ) ,则( )
,则( )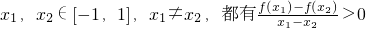 ,则
,则