| 函数f(x)=x2+x-lnx的极值点的个数是( ) |
相关习题
科目:高中数学
来源:
题型:
函数f(x)=x2+x-lnx的极值点的个数是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数f(x)=x
2+x-lnx的极值点的个数是( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省嘉兴市高二(下)期末数学试卷(文科)(解析版)
题型:选择题
函数f(x)=x2+x-lnx的极值点的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)=x
2-x,g(x)=lnx.
(1)求证:f(x)≥g(x);
(2)若f(x)≥ag(x)恒成立,求实数a的值;
(3)设F(x)=f(x)+mg(x)(m∈R)有两个极值点x
1、x
2(x
1<x
2);求实数m的取值范围,并证明:
F(x2)>-.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数f(x)=x
2-x,g(x)=lnx.
(1)求证:f(x)≥g(x);
(2)若f(x)≥ag(x)恒成立,求实数a的值;
(3)设F(x)=f(x)+mg(x)(m∈R)有两个极值点x
1、x
2(x
1<x
2);求实数m的取值范围,并证明:
F(x2)>-.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省重点中学联谊学校高三(上)期中数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=x
2-x,g(x)=lnx.
(1)求证:f(x)≥g(x);
(2)若f(x)≥ag(x)恒成立,求实数a的值;
(3)设F(x)=f(x)+mg(x)(m∈R)有两个极值点x
1、x
2(x
1<x
2);求实数m的取值范围,并证明:
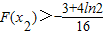
.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年广东省广州市增城中学高三(上)综合测试数学试卷4(理科)(解析版)
题型:解答题
已知函数f(x)=x
2-x,g(x)=lnx.
(1)求证:f(x)≥g(x);
(2)若f(x)≥ag(x)恒成立,求实数a的值;
(3)设F(x)=f(x)+mg(x)(m∈R)有两个极值点x
1、x
2(x
1<x
2);求实数m的取值范围,并证明:

.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年浙江省杭州地区七校联考高三(上)期中数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=x
2-x,g(x)=lnx.
(1)求证:f(x)≥g(x);
(2)若f(x)≥ag(x)恒成立,求实数a的值;
(3)设F(x)=f(x)+mg(x)(m∈R)有两个极值点x
1、x
2(x
1<x
2);求实数m的取值范围,并证明:

.
查看答案和解析>>
科目:高中数学
来源:2013年北京市高考数学预测试卷(八)(解析版)
题型:解答题
已知函数f(x)=x
2-x,g(x)=lnx.
(1)求证:f(x)≥g(x);
(2)若f(x)≥ag(x)恒成立,求实数a的值;
(3)设F(x)=f(x)+mg(x)(m∈R)有两个极值点x
1、x
2(x
1<x
2);求实数m的取值范围,并证明:

.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)=x
2-ax,g(x)=lnx
(1)若f(x)≥g(x)对于定义域内的x恒成立,求实数a的取值范围;
(2)设h(x)=f(x)+g(x)有两个极值点x
1,x
2且x
1∈(0,
),求证:h(x
1)-h(x
2)>
-ln2;
(3)设r(x)=f(x)+g(
),若对任意的a∈(1,2),总存在x
0∈[
,1],使不等式r(x
0)>k(1-a
2)成立,求实数k的取值范围.
查看答案和解析>>

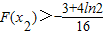 .
. .
. .
. .
.