练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （理科做）函数y=f（x）的图象关于直线y=x对称，向左平移一个长度单位后仍关于直线y=x对称，若f（1）=0，则f（2011）=（　　）
    A．-2010B．2010C．-2011D．2011
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    （理科做）函数y=f（x）的图象关于直线y=x对称，向左平移一个长度单位后仍关于直线y=x对称，若f（1）=0，则f（2011）=（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    （理科做）函数y=f（x）的图象关于直线y=x对称，向左平移一个长度单位后仍关于直线y=x对称，若f（1）=0，则f（2011）=（　　）
    A．-2010B．2010C．-2011D．2011

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年青海省湟川中学高三（上）第二次月考数学试卷（解析版） 题型：选择题

    （理科做）函数y=f（x）的图象关于直线y=x对称，向左平移一个长度单位后仍关于直线y=x对称，若f（1）=0，则f（2011）=（ ）
    A．-2010
    B．2010
    C．-2011
    D．2011

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    （理科做）函数y=f（x）的图象关于直线y=x对称，向左平移一个长度单位后仍关于直线y=x对称，若f（1）=0，则f（2011）=


    1. A.
      -2010
    2. B.
      2010
    3. C.
      -2011
    4. D.
      2011

    查看答案和解析>>

    科目：高中数学 来源：模拟题 题型：证明题

    已知点P（t，y）在函数f（x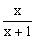）=（x≠-1）的图象上，且有t2-c2at+4c2=0（c≠0），
    （1）求证：|ac|≥4；
    （2）求证：在（-1，+∞）上f（x）单调递增；
    （3）（仅理科做）求证：f（|a|）+f（|c|）>1。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （理科做）已知函数f（x）=x2-ax+3在（0，1）上为减函数，函数g（x）=x2-alnx在区间（1，2）上为增函数．
    （1）求实数a的值；
    （2）当-1＜m＜0时，判断方程f（x）=2g（x）+m的解的个数，并说明理由；
    （3）设函数y=f（bx）（其中0＜b＜1）的图象C1与函数y=g（x）的图象C2交于P、Q，过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N．证明：曲线C1在点M处的切线与曲线C2在点N处的切线不平行．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （理科做）已知函数f（x）=x2-ax+3在（0，1）上为减函数，函数g（x）=x2-alnx在区间（1，2）上为增函数．
    （1）求实数a的值；
    （2）当-1＜m＜0时，判断方程f（x）=2g（x）+m的解的个数，并说明理由；
    （3）设函数y=f（bx）（其中0＜b＜1）的图象C1与函数y=g（x）的图象C2交于P、Q，过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N．证明：曲线C1在点M处的切线与曲线C2在点N处的切线不平行．

    查看答案和解析>>

    科目：高中数学 来源：2010年湖北省高考数学模拟试卷（文理合卷）（解析版） 题型：解答题

    （理科做）已知函数f（x）=x2-ax+3在（0，1）上为减函数，函数g（x）=x2-alnx在区间（1，2）上为增函数．
    （1）求实数a的值；
    （2）当-1＜m＜0时，判断方程f（x）=2g（x）+m的解的个数，并说明理由；
    （3）设函数y=f（bx）（其中0＜b＜1）的图象C1与函数y=g（x）的图象C2交于P、Q，过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N．证明：曲线C1在点M处的切线与曲线C2在点N处的切线不平行．

    查看答案和解析>>


    同步练习册答案