
| 已知直线l1:ax-y+1=0与l2:x+ay+1=0,给出如下结论: ①不论a为何值时,l1与l2都互相垂直; ②当a变化时,l1与l2分别经过定点A(0,1)和B(-1,0); ③不论a为何值时,l1与l2都关于直线x+y=0对称; ④当a变化时,l1与l2的交点轨迹是以AB为直径的圆(除去原点). 其中正确的结论有( )
|
科目:高中数学 来源: 题型:
科目:高中数学 来源: 题型:
科目:高中数学 来源:不详 题型:填空题
科目:高中数学 来源:不详 题型:单选题
| A.①③ | B.①②④ | C.①③④ | D.①②③④ |
科目:高中数学 来源:2012-2013学年四川省成都七中高一(下)期末数学试卷(解析版) 题型:选择题
科目:高中数学 来源: 题型:填空题
科目:高中数学 来源:2012届四川省绵阳市高二上学期期末教学质量测试数学试题 题型:选择题
已知直线l1:ax-y+2a=0与l2:(2a-1)x+ay+a=0互相垂直,则实数a的值为
A.1 B.2 C.0或1 D.0或2
科目:高中数学 来源: 题型:解答题
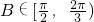 ,求
,求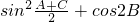 的取值范围.
的取值范围.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com