练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若在同一直角坐标系中，作y=x2，y=x2+2，y=-2x2+1的图象，则它们（　　）
    A．都关于y轴对称B．开口方向相同
    C．都经过原点D．互相可以通过平移得到
    A
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源：吴中区二模 题型：单选题

    若在同一直角坐标系中，作y=x2，y=x2+2，y=-2x2+1的图象，则它们（　　）
    A．都关于y轴对称B．开口方向相同
    C．都经过原点D．互相可以通过平移得到

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年安徽省安庆市桐城市黄冈初中九年级（上）月考数学试卷（10月份）（解析版） 题型：选择题

    若在同一直角坐标系中，作y=x2，y=x2+2，y=-2x2+1的图象，则它们（ ）
    A．都关于y轴对称
    B．开口方向相同
    C．都经过原点
    D．互相可以通过平移得到

    查看答案和解析>>

    科目：初中数学 来源：2012年江苏省苏州市吴中区中考数学二模试卷（解析版） 题型：选择题

    若在同一直角坐标系中，作y=x2，y=x2+2，y=-2x2+1的图象，则它们（ ）
    A．都关于y轴对称
    B．开口方向相同
    C．都经过原点
    D．互相可以通过平移得到

    查看答案和解析>>

    科目：初中数学 来源：2012年上海市卢湾区黄浦区中考数学一模试卷（解析版） 题型：选择题

    若在同一直角坐标系中，作y=x2，y=x2+2，y=-2x2+1的图象，则它们（ ）
    A．都关于y轴对称
    B．开口方向相同
    C．都经过原点
    D．互相可以通过平移得到

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    若在同一直角坐标系中，作y=x2，y=x2+2，y=-2x2+1的图象，则它们


    1. A.
      都关于y轴对称
    2. B.
      开口方向相同
    3. C.
      都经过原点
    4. D.
      互相可以通过平移得到

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•吴中区二模）若在同一直角坐标系中，作y=x2，y=x2+2，y=-2x2+1的图象，则它们（　　）

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2012年中考数学试题 题型：044

    在平面直角坐标系xOy中，已知二次函数y＝x2＋mx＋n的图象经过点A(2，0)和点B(1，－)，直线l经过抛物线的顶点且与y轴垂直，垂足为Q．

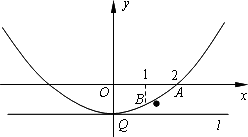
    (1)求该二次函数的表达式；

    (2)设抛物线上有一动点P从点B处出发沿抛物线向上运动，其纵坐标y1随时间t(t≥0)的变化规律为y1＝－＋2t．现以线段OP为直径作⊙C．

    ①当点P在起始位置点B处时，试判断直线l与⊙C的位置关系，并说明理由；在点P运动的过程中，直线l与⊙C是否始终保持这种位置关系？请说明你的理由；

    ②若在点P开始运动的同时，直线l也向上平行移动，且垂足Q的纵坐标y2随时间t的变化规律为y2＝－1＋3t，则当t在什么范围内变化时，直线l与⊙C相交？此时，若直线l被⊙C所截得的弦长为a，试求a2的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，点A（
    		3
    ，0），B（3
    		3
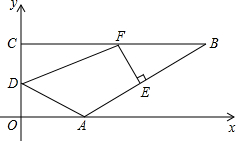    ，2），C（0，2）．动点D以每秒1个单位的速度从点O出发沿OC向终点C运动，同时动点E以每秒2个精英家教网单位的速度从点A出发沿AB向终点B运动．过点E作EF⊥AB，交BC于点F，连接DA、DF．设运动时间为t秒．
    （1）求∠ABC的度数；
    （2）当t为何值时，AB∥DF；
    （3）设四边形AEFD的面积为S．①求S关于t的函数关系式；
    ②若一抛物线y=-x2+mx经过动点E，当S＜2
    		3
    时，求m的取值范围（写出答案即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

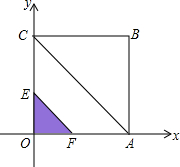    如图，在平面直角坐标系中，正方形ABCO的点A、C分别在x轴、y轴上，点B坐标为（6，6）连接AC．抛物线y=x2+bx+c经过B、C两点．
    （1）求抛物线的解析式．
    （2）若动点E从原点出发，以每秒一个单位的速度，沿折线O-C-B-A做匀速运动，同时点F从原点出发，以相同的速度向x正半轴方向做匀速运动，过点E作ED⊥x轴于点D，当点E停止运动时，点F也停止运动．设△EFD的面积为S，运动时间为x（0＜x＜18），试写出S与x的函数关系式，并求出S的最大值．
    （3）P是直线AC上的点，在抛物线上是否存在点Q，使以0、C、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》常考题集（20）：2.7 最大面积是多少（解析版） 题型：解答题

    如图，在平面直角坐标系中，点A（，0），B（3，2），C（0，2）．动点D以每秒1个单位的速度从点O出发沿OC向终点C运动，同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动．过点E作EF上AB，交BC于点F，连接DA、DF．设运动时间为t秒．
    （1）求∠ABC的度数；
    （2）当t为何值时，AB∥DF；
    （3）设四边形AEFD的面积为S．①求S关于t的函数关系式；
    ②若一抛物线y=-x2+mx经过动点E，当S＜2时，求m的取值范围（写出答案即可）．

    查看答案和解析>>


    同步练习册答案