直线y=x-2上的点在x轴的下方时对应的自变量的范围是

1. A.
   x＞2
2. B.
   x≥2
3. C.
   x＜2
4. D.
   x≤2

已知二次函数y=ax²+bx+c与自变量x的部分对应值如下表：

x	…	-1	0	1	3	…
y	…	-3	1	3	1	…

现给出下列说法：
①该函数开口向上．　②该函数图象的对称轴为过点（1，0）且平行于y轴的直线．
③当x=4时，y＜0．　 ④方程ax²+bx+c=0的正根在3与4之间．其中正确的说法为________．（只需写出序号）

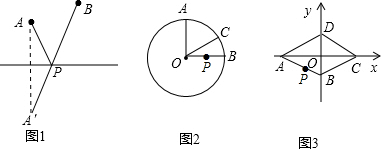
阅读材料：“最值问题”是数学中的一类较具挑战性的问题．其实，数学史上也有不少相关的故事，如下即为其中较为经典的一则：海伦是古希腊精通数学、物理的学者，相传有位将军曾向他请教一个问题--如图1，从A点出发，到笔直的河岸l去饮马，然后再去B地，走什么样的路线最短呢？海伦轻松地给出了答案：作点A关于直线l的对称点A′，连接A′B交l于点P，则PA+PB=A′B 的值最小．
解答问题：
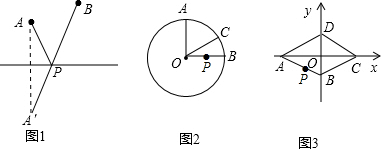
（1）如图2，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，求PA+PC的最小值；
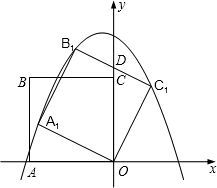
（2）如图3，已知菱形ABCD的边长为6，∠DAB=60°．将此菱形放置于平面直角坐标系中，各顶点恰好在坐标轴上．现有一动点P从点A出发，以每秒2个单位的速度，沿A→C的方向，向点C运动．当到达点C后，立即以相同的速度返回，返回途中，当运动到x轴上某一点M时，立即以每秒1个单位的速度，沿M→B的方向，向点B运动．当到达点B时，整个运动停止．
①为使点P能在最短的时间内到达点B处，则点M的位置应如何确定？
②在①的条件下，设点P的运动时间为t（s），△PAB的面积为S，在整个运动过程中，试求S与t之间的函数关系式，并指出自变量t的取值范围．