
若m<0,n>0,m+n<0,则m,n,-m,-n这四个数的大小关系是( )
|
科目:初中数学 来源: 题型:单选题

科目:初中数学 来源:不详 题型:单选题
| A.m>n>-n>-m | B.-m>n>-n>m | C.m>-m>n>-n | D.-m>-n>n>m |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
| k | x |

科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:填空题
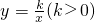 图象上,那么是否存在点C构成该反比例函数图象的伴侣正方形ABCD呢?________(填“是”或“否”),若存在,则猜想C点坐标为________.并求出m的值;若不存在,请说明理由.
图象上,那么是否存在点C构成该反比例函数图象的伴侣正方形ABCD呢?________(填“是”或“否”),若存在,则猜想C点坐标为________.并求出m的值;若不存在,请说明理由.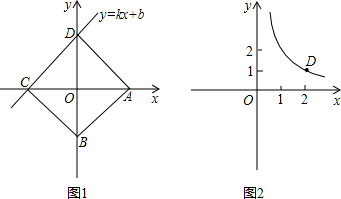
科目:初中数学 来源:2010年云南省德宏州中考数学试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:
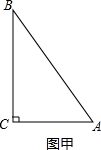 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.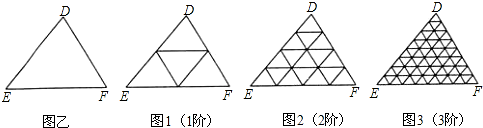
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com