
已知关于x的方程x2+kx+1=0和x2-x-k=0有一个根相同,则k的值为( )
|
科目:初中数学 来源: 题型:解答题
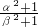 和
和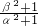 为根的一元二次方程.
为根的一元二次方程.科目:初中数学 来源:2007-2008学年江苏省苏州市常熟市九年级(上)期末数学试卷(解析版) 题型:选择题
科目:初中数学 来源:2004年全国中考数学试题汇编《一元二次方程》(04)(解析版) 题型:解答题
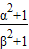 和
和 为根的一元二次方程.
为根的一元二次方程.科目:初中数学 来源:2004年江苏省扬州市中考数学试卷(解析版) 题型:解答题
 和
和 为根的一元二次方程.
为根的一元二次方程.科目:初中数学 来源: 题型:解答题
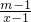 -
- =0无解,方程x2+kx+6=0的一个根是m.
=0无解,方程x2+kx+6=0的一个根是m.科目:初中数学 来源:2013年山东省济宁市中考数学试卷(解析版) 题型:解答题
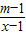 -
-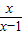 =0无解,方程x2+kx+6=0的一个根是m.
=0无解,方程x2+kx+6=0的一个根是m.科目:初中数学 来源:2013年山东省济宁市高级中等学校招生考试数学 题型:044
人教版教科书对分式方程验根的归纳如下:
“解分式方程时,去分母后所得整式方程的解有可能使原分式方程中的分母为0,因此应如下检验:将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.”
请你根据对这段话的理解,解决下面问题:
已知关于x的方程![]() -
-![]() =0无解,方程x2+kx+6=0的一个根是m.
=0无解,方程x2+kx+6=0的一个根是m.
(1)求m和k的值;
(2)求方程x2+kx+6=0的另一个根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com