相关习题
科目:高中数学
来源:2012-2013学年福建省厦门一中高二(上)期中数学试卷(理科)(解析版)
题型:选择题
对x∈R且x≠0都成立的不等式是( )
A.x

B.x

C.
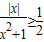
D.|x

|≥2
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知函数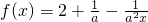 ,实数a∈R且a≠0.
,实数a∈R且a≠0.
(1)设mn>0,判断函数f(x)在[m,n]上的单调性,并说明理由;
(2)设0<m<n且a>0时,f(x)的定义域和值域都是[m,n],求n-m的最大值;
(3)若不等式|a2f(x)|≤2x对x≥1恒成立,求a的范围.
查看答案和解析>>
科目:高中数学
来源:0123 期末题
题型:解答题
已知函数
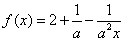
,实数a∈R且a≠0。
(1)设mn>0,令F(x)=af(x),讨论函数F(x)在[m,n]上单调性;
(2)设0<m<n且a>0时, f(x)的定义域和值域都是[m,n],求n-m的最大值;
(3)若不等式|a
2f(x)|≤2x对x≥1恒成立,求a的范围。
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省高三(上)10月段考数学试卷(文科)(解析版)
题型:解答题
(理)已知函数

,实数a∈R且a≠0.
(1)设mn>0,判断函数f(x)在[m,n]上的单调性,并说明理由;
(2)设0<m<n且a>0时,f(x)的定义域和值域都是[m,n],求n-m的最大值;
(3)若不等式|a
2f(x)|≤2x对x≥1恒成立,求a的范围.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省高三(上)10月段考数学试卷(文科)(解析版)
题型:解答题
(理)已知函数
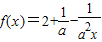
,实数a∈R且a≠0.
(1)设mn>0,判断函数f(x)在[m,n]上的单调性,并说明理由;
(2)设0<m<n且a>0时,f(x)的定义域和值域都是[m,n],求n-m的最大值;
(3)若不等式|a
2f(x)|≤2x对x≥1恒成立,求a的范围.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年四川省成都市新都一中高一(上)期末数学训练试卷(2)(解析版)
题型:解答题
(理)已知函数
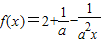
,实数a∈R且a≠0.
(1)设mn>0,判断函数f(x)在[m,n]上的单调性,并说明理由;
(2)设0<m<n且a>0时,f(x)的定义域和值域都是[m,n],求n-m的最大值;
(3)若不等式|a
2f(x)|≤2x对x≥1恒成立,求a的范围.
查看答案和解析>>
科目:高中数学
来源:2011年广东省高考数学模拟冲刺试卷(二)(解析版)
题型:解答题
(理)已知函数
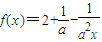
,实数a∈R且a≠0.
(1)设mn>0,判断函数f(x)在[m,n]上的单调性,并说明理由;
(2)设0<m<n且a>0时,f(x)的定义域和值域都是[m,n],求n-m的最大值;
(3)若不等式|a
2f(x)|≤2x对x≥1恒成立,求a的范围.
查看答案和解析>>
科目:高中数学
来源:2011年上海市长宁区高考数学一模试卷(理科)(解析版)
题型:解答题
(理)已知函数

,实数a∈R且a≠0.
(1)设mn>0,判断函数f(x)在[m,n]上的单调性,并说明理由;
(2)设0<m<n且a>0时,f(x)的定义域和值域都是[m,n],求n-m的最大值;
(3)若不等式|a
2f(x)|≤2x对x≥1恒成立,求a的范围.
查看答案和解析>>



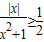
 |≥2
|≥2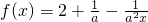 ,实数a∈R且a≠0.
,实数a∈R且a≠0.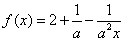 ,实数a∈R且a≠0。
,实数a∈R且a≠0。 ,实数a∈R且a≠0.
,实数a∈R且a≠0.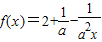 ,实数a∈R且a≠0.
,实数a∈R且a≠0.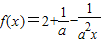 ,实数a∈R且a≠0.
,实数a∈R且a≠0.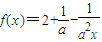 ,实数a∈R且a≠0.
,实数a∈R且a≠0. ,实数a∈R且a≠0.
,实数a∈R且a≠0.