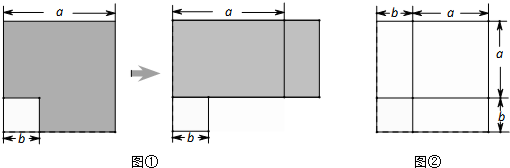
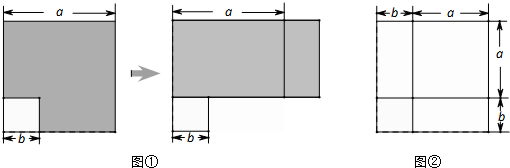
(2013•青岛)在前面的学习中,我们通过对同一面积的不同表达和比较,根据图1和图2发现并验证了平方差公式和完全平方公式.
这种利用面积关系解决问题的方法,使抽象的数量关系因几何直观而形象化.
【研究速算】
提出问题:47×43,56×54,79×71,…是一些十位数字相同,且个位数字之和是10的两个两位数相乘的算式,是否可以找到一种速算方法?
几何建模:
用矩形的面积表示两个正数的乘积,以47×43为例:
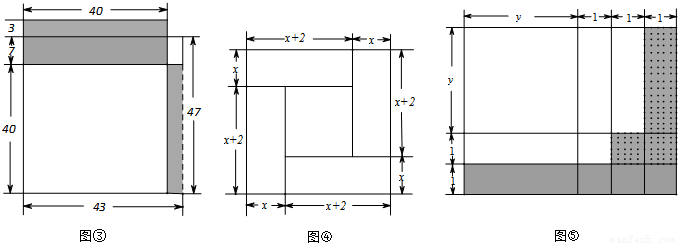
(1)画长为47,宽为43的矩形,如图3,将这个47×43的矩形从右边切下长40,宽3的一条,拼接到原矩形上面.
(2)分析:原矩形面积可以有两种不同的表达方式:47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的矩形面积之和,即47×43=(40+10)×40+3×7=5×4×100+3×7=2021.
用文字表述47×43的速算方法是:十位数字4加1的和与4相乘,再乘以100,加上个位数字3与7的积,构成运算结果.
归纳提炼:
两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是(用文字表述)
十位数字加1的和与十位数字相乘,再乘以100,加上两个个位数字的积,构成运算结果
十位数字加1的和与十位数字相乘,再乘以100,加上两个个位数字的积,构成运算结果
.
【研究方程】
提出问题:怎样图解一元二次方程x
2+2x-35=0(x>0)?
几何建模:
(1)变形:x(x+2)=35.
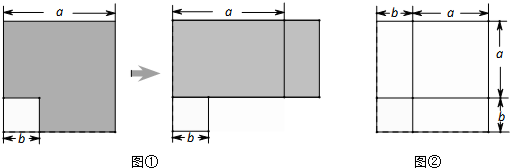
(2)画四个长为x+2,宽为x的矩形,构造图4
(3)分析:图中的大正方形面积可以有两种不同的表达方式,(x+x+2)
2或四个长x+2,宽x的矩形面积之和,加上中间边长为2的小正方形面积.
即(x+x+2)
2=4x(x+2)+2
2∵x(x+2)=35
∴(x+x+2)
2=4×35+2
2∴(2x+2)
2=144
∵x>0
∴x=5
归纳提炼:求关于x的一元二次方程x(x+b)=c(x>0,b>0,c>0)的解.
要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并注明相关线段的长)
【研究不等关系】
提出问题:怎样运用矩形面积表示(y+3)(y+2)与2y+5的大小关系(其中y>0)?
几何建模:
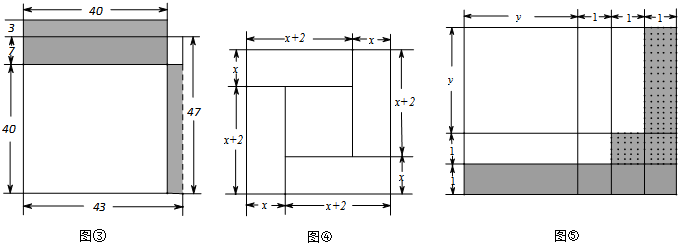
(1)画长y+3,宽y+2的矩形,按图5方式分割
(2)变形:2y+5=(y+3)+(y+2)
(3)分析:图5中大矩形的面积可以表示为(y+3)(y+2);阴影部分面积可以表示为(y+3)×1,画点部分部分的面积可表示为y+2,由图形的部分与整体的关系可知(y+3)(y+2)>(y+3)+(y+2),即(y+3)(y+2)>2y+5
归纳提炼:
当a>2,b>2时,表示ab与a+b的大小关系.
根据题意,设a=2+m,b=2+n(m>0,n>0),要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图并注明相关线段的长)