已知定义在R上奇函数f(x)满足f(1+x)=f(1-x)且f(x)在区间[-1,1]上单调递增,则函数f(x)在区间[1,3]上的( )| A.最大值是f(1),最小值是f(3) | | B.最大值是f(3),最小值是f(1) | | C.最大值是f(1),最小值是f(2) | | D.最大值是f(2),最小值是f(3) |
|
相关习题
科目:高中数学
来源:
题型:
8、已知定义在R上奇函数f(x)满足f(1+x)=f(1-x)且f(x)在区间[-1,1]上单调递增,则函数f(x)在区间[1,3]上的( )
查看答案和解析>>
科目:高中数学
来源:成都一模
题型:单选题
已知定义在R上奇函数f(x)满足f(1+x)=f(1-x)且f(x)在区间[-1,1]上单调递增,则函数f(x)在区间[1,3]上的( )
| A.最大值是f(1),最小值是f(3) |
| B.最大值是f(3),最小值是f(1) |
| C.最大值是f(1),最小值是f(2) |
| D.最大值是f(2),最小值是f(3) |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖南省常德市澧县一中高三(上)第二次周考数学试卷(理科)(解析版)
题型:选择题
已知定义在R上奇函数f(x)满足f(1+x)=f(1-x)且f(x)在区间[-1,1]上单调递增,则函数f(x)在区间[1,3]上的( )
A.最大值是f(1),最小值是f(3)
B.最大值是f(3),最小值是f(1)
C.最大值是f(1),最小值是f(2)
D.最大值是f(2),最小值是f(3)
查看答案和解析>>
科目:高中数学
来源:2012-2013学年河南省郑州市新密二高高三(上)周练数学试卷3(理科)(解析版)
题型:选择题
已知定义在R上奇函数f(x)满足①对任意x,都有f(x+3)=f(x)成立;②当

时

,则

在[-4,4]上根的个数是( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省临沂市罗庄高考补习学校高三(上)10月月考数学试卷(理科)(解析版)
题型:选择题
已知定义在R上奇函数f(x)满足①对任意x,都有f(x+3)=f(x)成立;②当
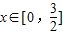
时
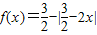
,则
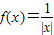
在[-4,4]上根的个数是( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖南省常德市澧县一中高三(上)第二次周考数学试卷(理科)(解析版)
题型:选择题
已知定义在R上奇函数f(x)满足f(1+x)=f(1-x)且f(x)在区间[-1,1]上单调递增,则函数f(x)在区间[1,3]上的( )
A.最大值是f(1),最小值是f(3)
B.最大值是f(3),最小值是f(1)
C.最大值是f(1),最小值是f(2)
D.最大值是f(2),最小值是f(3)
查看答案和解析>>
科目:高中数学
来源:2012-2013学年河南省郑州市新密二高高三(上)周练数学试卷3(理科)(解析版)
题型:选择题
已知定义在R上奇函数f(x)满足①对任意x,都有f(x+3)=f(x)成立;②当
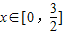
时

,则
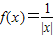
在[-4,4]上根的个数是( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学
来源:2012年山东省日照市高考数学一模试卷(理科)(解析版)
题型:选择题
已知定义在R上奇函数f(x)满足①对任意x,都有f(x+3)=f(x)成立;②当

时

,则

在[-4,4]上根的个数是( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学
来源:2010年四川省成都市高考数学一模试卷(理科)(解析版)
题型:选择题
已知定义在R上奇函数f(x)满足f(1+x)=f(1-x)且f(x)在区间[-1,1]上单调递增,则函数f(x)在区间[1,3]上的( )
A.最大值是f(1),最小值是f(3)
B.最大值是f(3),最小值是f(1)
C.最大值是f(1),最小值是f(2)
D.最大值是f(2),最小值是f(3)
查看答案和解析>>
科目:高中数学
来源:2011年重庆十一中高考数学一模训练试卷(一)(解析版)
题型:选择题
已知定义在R上奇函数f(x)满足f(1+x)=f(1-x)且f(x)在区间[-1,1]上单调递增,则函数f(x)在区间[1,3]上的( )
A.最大值是f(1),最小值是f(3)
B.最大值是f(3),最小值是f(1)
C.最大值是f(1),最小值是f(2)
D.最大值是f(2),最小值是f(3)
查看答案和解析>>

 时
时 ,则
,则 在[-4,4]上根的个数是( )
在[-4,4]上根的个数是( )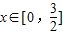 时
时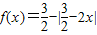 ,则
,则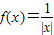 在[-4,4]上根的个数是( )
在[-4,4]上根的个数是( )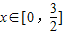 时
时 ,则
,则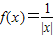 在[-4,4]上根的个数是( )
在[-4,4]上根的个数是( ) 时
时 ,则
,则 在[-4,4]上根的个数是( )
在[-4,4]上根的个数是( )