
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题

科目:初中数学 来源:2011年中考复习专项训练《实验与操作》(解析版) 题型:解答题
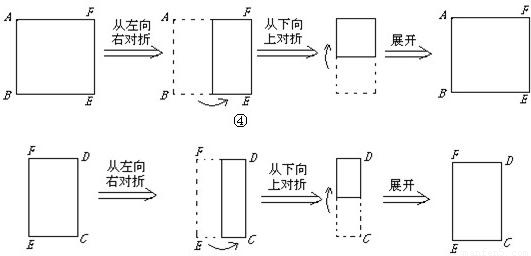
科目:初中数学 来源:2010年河北省保定市博野县中考数学二模试卷(解析版) 题型:解答题

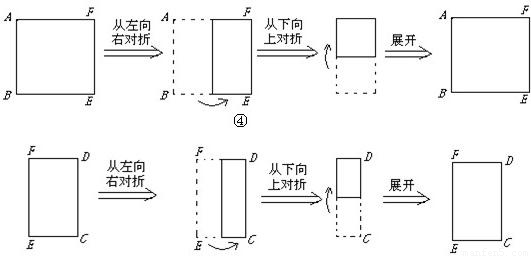
科目:初中数学 来源: 题型:
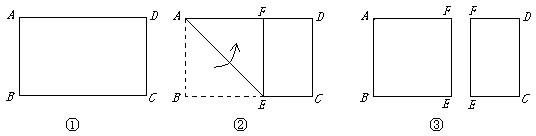
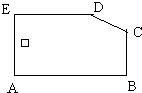 18、如图,已知五边形ABCDE中,AB∥ED,∠A=∠B=90°,则可以将五边形ABCDE分成面积相等的两部分的直线有
18、如图,已知五边形ABCDE中,AB∥ED,∠A=∠B=90°,则可以将五边形ABCDE分成面积相等的两部分的直线有科目:初中数学 来源: 题型:
如图,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B左侧),与y轴交
轴交于A、B两点(点A在点B左侧),与y轴交
于点C,且当![]() =0和
=0和![]() =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
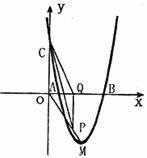
(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥![]() 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
科目:初中数学 来源:2008年初中毕业升学考试(河南濮阳卷)数学(带解析) 题型:解答题
如图,抛物线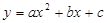 与
与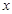 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当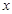 =O和
=O和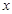 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。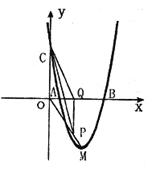
(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥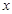 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com