
点C在线段AB上,不能判断点C是线段AB中点的式子是( )
|
科目:初中数学 来源: 题型:解答题
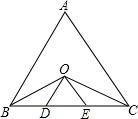 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.科目:初中数学 来源: 题型:
| 3 |
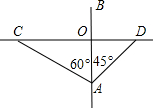 小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?
小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?科目:初中数学 来源: 题型:解答题
 =1.732)
=1.732)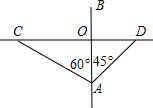 小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?
小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?科目:初中数学 来源:2012年安徽省中考数学模拟试卷(四)(解析版) 题型:解答题
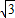 =1.732)
=1.732)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com