
设△ABC的三边为a,b,c,三边上的高分别为ha,hb,hc,若三边满足2b=a+c,则三个高应满足( )
|
科目:初中数学 来源:不详 题型:单选题
| A.2hb=ha+hc | B.
| ||||||
C.
| D.以上关系均不对 |
科目:初中数学 来源:2007年安徽省马鞍山市第二中学理科实验班招生数学试卷(解析版) 题型:选择题


科目:初中数学 来源: 题型:单选题
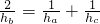
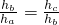
科目:初中数学 来源: 题型:
| 1 |
| ha |
| 1 |
| hb |
| 1 |
| hc |
科目:初中数学 来源:不详 题型:单选题
| 1 |
| ha |
| 1 |
| hb |
| 1 |
| hc |
A.
| B.
| C.
| D.
|
科目:初中数学 来源: 题型:
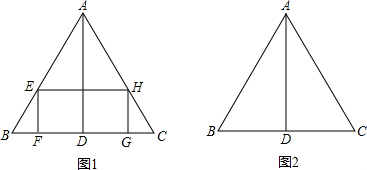
科目:初中数学 来源: 题型:解答题
 ,以BC边所在直线为x轴,BC边上的高线AO所在的直线为y轴建立平面直角坐标系.
,以BC边所在直线为x轴,BC边上的高线AO所在的直线为y轴建立平面直角坐标系.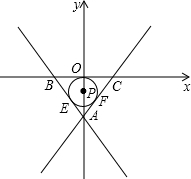
科目:初中数学 来源: 题型:
如图,等边三角形ABC,边长为2,AD是BC边上的高.
(1)在△ABC内部作一个矩形EFGH(如图1),其中E、H分别在边AB、AC上,FG在边BC上。①设矩形的一边FG=x,那么EF= .(用含有x的代数式表示)
②设矩形的面积为y,当x取何值时,y的值最大?最大值是多少?
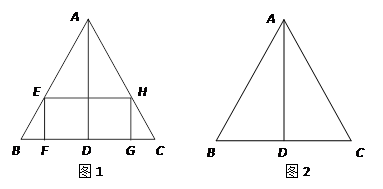 (2)在图2中,只用圆规画出点E,使得上述矩形EFGH面积最大.写出画法,并保留作图痕迹.
(2)在图2中,只用圆规画出点E,使得上述矩形EFGH面积最大.写出画法,并保留作图痕迹.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com