下列说法错误的是( )| A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5 | | B.反比例函数y=的图象经过点(1,2) | | C.函数y=3x中,y随着x的增大而减小 | | D.抛物线y=x2-2x+1的对称轴是x=1 |
|
相关习题
科目:初中数学
来源:铜仁地区
题型:单选题
下列说法错误的是( )
| A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5 |
| B.反比例函数y=的图象经过点(1,2) |
| C.函数y=3x中,y随着x的增大而减小 |
| D.抛物线y=x2-2x+1的对称轴是x=1 |
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(05):2.4 二次函数y=ax2+bx+c的图象(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数

的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>
科目:初中数学
来源:第34章《二次函数》中考题集(05):34.3 二次函数的图象和性质(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数

的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(04):2.2 二次函数的图象与性质(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数

的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>
科目:初中数学
来源:第6章《二次函数》中考题集(04):6.2 二次函数的图象和性质(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数

的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>
科目:初中数学
来源:第27章《二次函数》中考题集(04):27.2 二次函数的图象与性质(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数
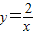
的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>
科目:初中数学
来源:第26章《二次函数》中考题集(03):26.1 二次函数(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数
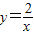
的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(04):2.4 二次函数y=ax2+bx+c的图象和性质(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数

的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>
科目:初中数学
来源:第20章《二次函数和反比例函数》中考题集(63):20.7 反比例函数的图象、性质和应用(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数
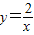
的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(10):2.3 二次函数的性质(解析版)
题型:选择题
下列说法错误的是( )
A.已知一次函数的图象经过两点A(5,0),B(0,5),则这个函数的解析式是y=-x+5
B.反比例函数

的图象经过点(1,2)
C.函数y=3x中,y随着x的增大而减小
D.抛物线y=x
2-2x+1的对称轴是x=1
查看答案和解析>>

 的图象经过点(1,2)
的图象经过点(1,2) 的图象经过点(1,2)
的图象经过点(1,2) 的图象经过点(1,2)
的图象经过点(1,2) 的图象经过点(1,2)
的图象经过点(1,2)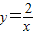 的图象经过点(1,2)
的图象经过点(1,2)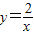 的图象经过点(1,2)
的图象经过点(1,2) 的图象经过点(1,2)
的图象经过点(1,2)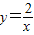 的图象经过点(1,2)
的图象经过点(1,2) 的图象经过点(1,2)
的图象经过点(1,2)