下列四个命题,
①如果两个平面有三个公共点,那么这两个平面重合;
②如果两条直线不重合,那么他们可以确定一个平面;
③若l?α,A∈l,则A?α;
④若P∈α,P∈β,α∩β=l,则P∈l.
其中真命题的个数为( ) |
相关习题
科目:高中数学
来源:
题型:
下列四个命题,
①如果两个平面有三个公共点,那么这两个平面重合;
②如果两条直线不重合,那么他们可以确定一个平面;
③若l?α,A∈l,则A∉α;
④若P∈α,P∈β,α∩β=l,则P∈l.
其中真命题的个数为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
下列四个命题,
①如果两个平面有三个公共点,那么这两个平面重合;
②如果两条直线不重合,那么他们可以确定一个平面;
③若l?α,A∈l,则A∉α;
④若P∈α,P∈β,α∩β=l,则P∈l.
其中真命题的个数为( )
查看答案和解析>>
科目:高中数学
来源:2009-2010学年北京师大附中高一(下)期末数学试卷(解析版)
题型:选择题
下列四个命题,
①如果两个平面有三个公共点,那么这两个平面重合;
②如果两条直线不重合,那么他们可以确定一个平面;
③若l?α,A∈l,则A∉α;
④若P∈α,P∈β,α∩β=l,则P∈l.
其中真命题的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
下列四个命题,
①如果两个平面有三个公共点,那么这两个平面重合;
②如果两条直线不重合,那么他们可以确定一个平面;
③若l?α,A∈l,则A∉α;
④若P∈α,P∈β,α∩β=l,则P∈l.
其中真命题的个数为
- A.
1个
- B.
2个
- C.
3个
- D.
4个
查看答案和解析>>
科目:高中数学
来源:
题型:
2、给出下列四个命题:
①如果两个平面有三个公共点,那么这两个平面重合;
②两条直线可以确定一个平面;
③若M∈α,M∈β,α∩β=l,则M∈l;
④空间中,相交于同一点的三条直线在同一平面内.
其中真命题的个数为
1
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
给出下列四个命题:
①如果两个平面有三个公共点,那么这两个平面重合;
②两条直线可以确定一个平面;
③若M∈α,M∈β,α∩β=l,则M∈l;
④空间中,相交于同一点的三条直线在同一平面内.
其中真命题的个数为
______.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
给出下列四个命题:
①如果两个平面有三个公共点,那么这两个平面重合;
②两条直线可以确定一个平面;
③若M∈α,M∈β,α∩β=l,则M∈l;
④空间中,相交于同一点的三条直线在同一平面内.
其中真命题的个数为
______.
查看答案和解析>>
科目:高中数学
来源:《第1章 空间几何体》2010年单元测试卷(2)(解析版)
题型:填空题
给出下列四个命题:
①如果两个平面有三个公共点,那么这两个平面重合;
②两条直线可以确定一个平面;
③若M∈α,M∈β,α∩β=l,则M∈l;
④空间中,相交于同一点的三条直线在同一平面内.
其中真命题的个数为 .
查看答案和解析>>
科目:高中数学
来源:2010年福建省高考数学一轮复习:14.2 空间图形的基本关系与公理(解析版)
题型:解答题
给出下列四个命题:
①如果两个平面有三个公共点,那么这两个平面重合;
②两条直线可以确定一个平面;
③若M∈α,M∈β,α∩β=l,则M∈l;
④空间中,相交于同一点的三条直线在同一平面内.
其中真命题的个数为 .
查看答案和解析>>
科目:高中数学
来源:2010年广东省高三上学期期中考试文科数学卷
题型:选择题
下列四个命题中,真命题的个数为(
)
(1)如果两个平面有三个公共点,那么这两个平面重合;
(2)两条直线可以确定一个平面;
(3)若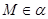 ,
, ,
, ,则
,则 ;
;
(4)空间中,相交于同一点的三直线在同一平面内.
A.1
B.2 C.3 D.4
查看答案和解析>>

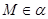 ,
, ,
, ,则
,则 ;
;