
下面列出的不等式中,正确的是( )
|
科目:初中数学 来源:不详 题型:单选题
| A.a不是负数,可表示成a>0 |
| B.x不大于3,可表示成x<3 |
| C.m与4的差是负数,可表示成m-4<0 |
| D.x与2的和是非负数,可表示成x+2>0 |
科目:初中数学 来源: 题型:解答题
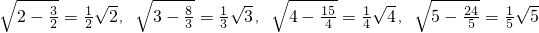 ,…
,…科目:初中数学 来源: 题型:
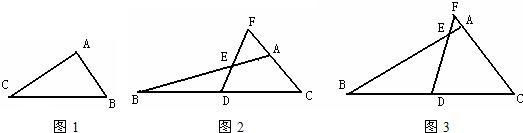 23、(1)如图1,在△ABC中,绕点C旋转180°后,得到△CA′B′请先画出变换后的图形,写出下列结论正确的序号是
23、(1)如图1,在△ABC中,绕点C旋转180°后,得到△CA′B′请先画出变换后的图形,写出下列结论正确的序号是科目:初中数学 来源:广西自治区中考真题 题型:解答题
科目:初中数学 来源: 题型:
2-
|
| 1 |
| 2 |
| 2 |
3-
|
| 1 |
| 3 |
| 3 |
4-
|
| 1 |
| 4 |
| 4 |
5-
|
| 1 |
| 5 |
| 5 |
科目:初中数学 来源:不详 题型:解答题
2-
|
| 1 |
| 2 |
| 2 |
3-
|
| 1 |
| 3 |
| 3 |
4-
|
| 1 |
| 4 |
| 4 |
5-
|
| 1 |
| 5 |
| 5 |
科目:初中数学 来源: 题型:解答题
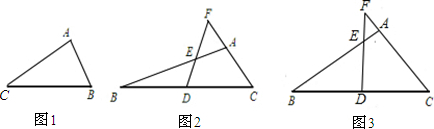
科目:初中数学 来源:2009年江苏省盐城市盐都区中考数学二模试卷(解析版) 题型:解答题

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com