
已知等腰三角形ABC的底边BC=5,且|AC-BC|=2,那么腰AC的长为( )
|
科目:初中数学 来源:新课程同步练习 数学 八年级上册 题型:013
已知等腰三角形ABC的底边BC=8 cm,且|AC-BC|=2 cm,则腰AC的长为
A.10 cm或6 cm
B.10 cm
C.6 cm
D.8 cm或6 cm
科目:初中数学 来源:101网校同步练习 初一数学 华东师大(新课标2001-3年初审) 华东师大(新课标2001-3年初审) 题型:013
已知等腰三角形△ABC的底边BC=8 cm,且|AC-BC|=2 cm,那么腰AC的长为
A.8 cm
B.10 cm
C.10 cm或6 cm
D.8 cm或6 cm
科目:初中数学 来源:青岛版(2014) 七年级下 题型:
| |||||
科目:初中数学 来源: 题型:解答题
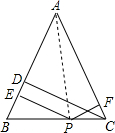 求证:等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.
求证:等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.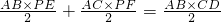
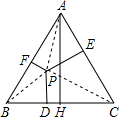
科目:初中数学 来源: 题型:解答题
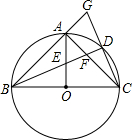 AC分别交于点E、F延长BA、CD交于G.
AC分别交于点E、F延长BA、CD交于G.科目:初中数学 来源: 题型:
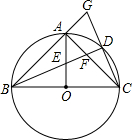 AC分别交于点E、F延长BA、CD交于G.
AC分别交于点E、F延长BA、CD交于G.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com