
将直线y=-2x向左平移1个单位所得的直线的解析式是( )
|
科目:初中数学 来源:不详 题型:单选题
| A.y=-2x+1 | B.y=-2x-1 | C.y=-2(x+1) | D.y=-2(x-1) |
科目:初中数学 来源:中考必备’04全国中考试题集锦·数学 题型:044
阅读以下材料并完成后面的问题.
将直线y=2x-3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
解:在直线y=2x-3上任取两点A(1,-1)、B(0,-3).
由题意知:
点A向右平移3个单位得![]() (4,-1);再向上平移1个单位得
(4,-1);再向上平移1个单位得![]() (4,0).
(4,0).
点B向右平移3个单位得![]() (3,-3);再向上平移1个单位得
(3,-3);再向上平移1个单位得![]() (3,-2).
(3,-2).
设平移后的直线的解析式为y=kx+b.
则点![]() (4,0)、
(4,0)、![]() (3,-2)在该直线上,
(3,-2)在该直线上,
可解得k=2,b=-8.
所以平移后的直线的解析式为y=2x-8.
根据以上信息解答下面问题:
将二次函数y=-x2+2x+3的图像向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式.(平移后抛物线形状不变)
科目:初中数学 来源: 题型:阅读理解
科目:初中数学 来源: 题型:填空题
科目:初中数学 来源: 题型:
 已知二次函数y=x2-2x-3
已知二次函数y=x2-2x-3| x | … | … | |||||
| y=x2-2x-3 | … | … |
科目:初中数学 来源: 题型:解答题
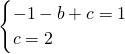 ,解得:
,解得: .所以平移后的抛物线的解析式为:y=-x2+2.
.所以平移后的抛物线的解析式为:y=-x2+2.科目:初中数学 来源:2013年四川省凉山州中考数学试卷(解析版) 题型:解答题
 ,解得:
,解得: .所以平移后的抛物线的解析式为:y=-x2+2.
.所以平移后的抛物线的解析式为:y=-x2+2.科目:初中数学 来源:2013年四川省凉山州高级中等学校招生考试数学 题型:044
先阅读以下材料,然后解答问题:
材料:将二次函数y=-x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).
解:在抛物线y=-x2+2x+3撒谎个任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到![]() (-1,3),再向下平移2个单位得到
(-1,3),再向下平移2个单位得到![]() (-1,1);点B向左平移1个单位得到
(-1,1);点B向左平移1个单位得到![]() (0,4),再向下平移2个单位得到
(0,4),再向下平移2个单位得到![]() (0,2).
(0,2).
设平移后的抛物线的解析式为y=-x2+bx+c.
则点![]() (-1,1),
(-1,1),![]() (0,2)在抛物线上.
(0,2)在抛物线上.
可得:![]() ,解得:
,解得:![]() .
.
所以平移后的抛物线的解析式为:y=-x2+2.
根据以上信息解答下列问题:
将直线y=2x-3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
科目:初中数学 来源: 题型:阅读理解
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com