练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知集合A={a，b，c}，B={-1，0，1}，定义：f是一个确定的对应关系，如果?x∈A
    ，?y∈B
    使y=f（x），且y唯一确定，那么就称f是集合A到B的一个映射．则满足f（a）+f（b）+f（c）＞0的映射f的个数是（　　）
    A．10B．9C．8D．7
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    已知集合A={a，b，c}，B={-1，0，1}，定义：f是一个确定的对应关系，如果?x∈A
    ，?y∈B
    使y=f（x），且y唯一确定，那么就称f是集合A到B的一个映射．则满足f（a）+f（b）+f（c）＞0的映射f的个数是（　　）
    A、10B、9C、8D、7

    查看答案和解析>>

    科目：高中数学 来源：门头沟区一模 题型：单选题

    已知集合A={a，b，c}，B={-1，0，1}，定义：f是一个确定的对应关系，如果?x∈A
    ，?y∈B
    使y=f（x），且y唯一确定，那么就称f是集合A到B的一个映射．则满足f（a）+f（b）+f（c）＞0的映射f的个数是（　　）
    A．10B．9C．8D．7

    查看答案和解析>>

    科目：高中数学 来源：2010年北京市门头沟区高考数学一模试卷（文科）（解析版） 题型：选择题

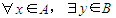    已知集合A={a，b，c}，B={-1，0，1}，定义：f是一个确定的对应关系，如果使y=f（x），且y唯一确定，那么就称f是集合A到B的一个映射．则满足f（a）+f（b）+f（c）＞0的映射f的个数是（ ）
    A．10
    B．9
    C．8
    D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：022

    已知集合A={a，b，c}，B={－1，0，1，2}，f是A到B的映射，且满足f(a)＋f(b)＋f(c)=0，则这样的映射有_______个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    已知集合A={a，b，c}，B={－1，0，1}，建立映射f：A→B，设a的象是f(a)，b的象是f(b)，c的象是f(c)，则满足f(a)=f(b)＋f(c)的映射有几个？

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：022

    已知集合A={a，b，c}，B={－1，0，1，2}，f是A到B的映射，且满足f(a)＋f(b)＋f(c)=0，则这样的映射有_______个．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    已知集合A={a，b，c}，B={－1，0，1}，建立映射f：A→B，设a的象是f(a)，b的象是f(b)，c的象是f(c)，则满足f(a)=f(b)＋f(c)的映射有几个？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合A={a，b，c，d，e}，B={-1，0，1}，则从集合A到集合B的不同映射有（　　）个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合M={a，b，c}，N={-1，0，1}，若f是M→N的映射，且f（a）=0，则这样的映射共有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合M={a，b，c}，N={-1，0，1}，从M到N的映射满足f（a）+f（b）+f（c）=0，那么映射f的个数为（　　）

    查看答案和解析>>


    同步练习册答案