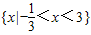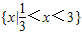已知函数y=f(x-1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线x-y=0对称,那么y=g(x)的对称中心为( )| A.(1,0) | B.(-1,0) | C.(0,1) | D.(0,-1) |
|
相关习题
科目:高中数学
来源:湖北模拟
题型:单选题
已知函数y=f(x-1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线x-y=0对称,那么y=g(x)的对称中心为( )
| A.(1,0) | B.(-1,0) | C.(0,1) | D.(0,-1) |
查看答案和解析>>
科目:高中数学
来源:2007-2008学年湖北省部分重点中学高三第一次联考数学试卷(文科)(解析版)
题型:选择题
已知函数y=f(x-1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线x-y=0对称,那么y=g(x)的对称中心为( )
A.(1,0)
B.(-1,0)
C.(0,1)
D.(0,-1)
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知函数y=f(x-1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线x-y=0对称,那么y=g(x)的对称中心为
- A.
(1,0)
- B.
(-1,0)
- C.
(0,1)
- D.
(0,-1)
查看答案和解析>>
科目:高中数学
来源:
题型:
8、已知函数y=f(2x+1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称,则g(x)+g(-x)的值为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数y=f(x+1)是定义域为R的偶函数,且在[1,+∞)上单调递增,则不等式f(2x-1)<f(x+2)的解集为( )
| A、{x|x<3} |
| B、{x|<x<3} |
| C、{x|-<x<3} |
| D、{x|<x<3} |
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知函数y=f(2x+1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称,则g(x)+g(-x)的值为
- A.
2
- B.
0
- C.
1
- D.
不能确定
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数y=f(2x+1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称,则g(x)+g(-x)的值为( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省蚌埠市蚌山二中高一(上)期中数学试卷(解析版)
题型:选择题
已知函数y=f(2x+1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称,则g(x)+g(-x)的值为( )
A.2
B.0
C.1
D.不能确定
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省蚌埠市蚌山二中高一(上)期中数学试卷(解析版)
题型:选择题
已知函数y=f(2x+1)是定义在R上的奇函数,函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称,则g(x)+g(-x)的值为( )
A.2
B.0
C.1
D.不能确定
查看答案和解析>>
科目:高中数学
来源:2011-2012学年宁夏银川一中高三(下)第五次月考数学试卷(理科)(解析版)
题型:选择题
已知函数y=f(x+1)是定义域为R的偶函数,且在[1,+∞)上单调递增,则不等式f(2x-1)<f(x+2)的解集为( )
A.{x|x<3}
B.

C.
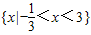
D.
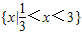
查看答案和解析>>