| 已知数列{an}的前n项和Sn=2-2n+1,则a3=( ) |
相关习题
科目:高中数学
来源:
题型:
已知数列{an}的前n项和Sn=2-2n+1,则a3=( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列{a
n}的前n项和
Sn=2-2n+1,则a
3=( )
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}的前n项和
Sn=(2n-1),数列{b
n}满足b
n=log
2a
n,则T
n=(b
1)
2-(b
2)
2+(b
3)
2+…++(-1)
n-1(b
n)
2(n∈N
*)可化简为
.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}的前n项和S
n=2a
n-2
n+1+2(n∈N
*).
(Ⅰ)设
bn=,求证数列{b
n}是等差数列,并求数列{a
n}的通项公式;
(Ⅱ)令
cn=,T
n=c
1+c
2+…+c
n,求证:T
n≥1(n∈N
*).
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}的前n项和S
n=2a
n-2
n+1+2(n为正整数).
(1)求数列{a
n}的通项公式;
(2)令b
n=log
2a
1+
log2+…+
log2,求数列{
}的前n项和T
n.
查看答案和解析>>
科目:高中数学
来源:云南省模拟题
题型:解答题
已知数列{a
n}的前n项和S
n=2a
n-2
n+1。
(1)证明:数列
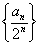
是等差数列;
(2)若不等式a
n+1<(5-λ)a
n恒成立,求λ的取值范围。
查看答案和解析>>
科目:高中数学
来源:2010年河南省豫南九校高考数学仿真模拟试卷(理科)(解析版)
题型:解答题
已知数列{a
n}的前n项和S
n=2a
n-2
n+1+2(n∈N
*).
(Ⅰ)设

,求证数列{b
n}是等差数列,并求数列{a
n}的通项公式;
(Ⅱ)令

,T
n=c
1+c
2+…+c
n,求证:T
n≥1(n∈N
*).
查看答案和解析>>
科目:高中数学
来源:2010年四川省攀枝花市高考数学三模试卷(理科)(解析版)
题型:解答题
已知数列{a
n}的前n项和S
n=2a
n-2
n+1+2(n∈N
*).
(Ⅰ)设
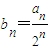
,求证数列{b
n}是等差数列,并求数列{a
n}的通项公式;
(Ⅱ)令

,T
n=c
1+c
2+…+c
n,求证:T
n≥1(n∈N
*).
查看答案和解析>>
科目:高中数学
来源:2010年四川省攀枝花市高考数学三模试卷(文科)(解析版)
题型:解答题
已知数列{a
n}的前n项和S
n=2a
n-2
n+1+2(n∈N
*).
(Ⅰ)设

,求证数列{b
n}是等差数列,并求数列{a
n}的通项公式;
(Ⅱ)令

,T
n=c
1+c
2+…+c
n,求证:T
n≥1(n∈N
*).
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}的前n项和S
n=2
n,数列{b
n}满足b
1=-1,b
n+1=b
n+(2n-1)(n=1,2,3,…).
(1)求数列{a
n}的通项a
n;
(2)求数列{b
n}的通项b
n;
(3)若
cn=,求数列{c
n}的前n项和T
n.
查看答案和解析>>

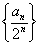 是等差数列;
是等差数列; ,求证数列{bn}是等差数列,并求数列{an}的通项公式;
,求证数列{bn}是等差数列,并求数列{an}的通项公式; ,Tn=c1+c2+…+cn,求证:Tn≥1(n∈N*).
,Tn=c1+c2+…+cn,求证:Tn≥1(n∈N*).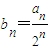 ,求证数列{bn}是等差数列,并求数列{an}的通项公式;
,求证数列{bn}是等差数列,并求数列{an}的通项公式; ,Tn=c1+c2+…+cn,求证:Tn≥1(n∈N*).
,Tn=c1+c2+…+cn,求证:Tn≥1(n∈N*). ,求证数列{bn}是等差数列,并求数列{an}的通项公式;
,求证数列{bn}是等差数列,并求数列{an}的通项公式; ,Tn=c1+c2+…+cn,求证:Tn≥1(n∈N*).
,Tn=c1+c2+…+cn,求证:Tn≥1(n∈N*).