（2012•李沧区一模）【问题引入】
几个人拎着水桶在一个水龙头前面排队打水，水桶有大有小．他们该怎样排队才能使得总的排队时间最短？
假设只有两个人时，设大桶接满水需要T分钟，小桶接满水需要t分钟（显然T＞t），若拎着大桶者在拎着小桶者之前，则拎大桶者可直接接水，只需等候T分钟，拎小桶者一共等候了（T+t）分钟，两人一共等候了（2T+t）分钟；反之，若拎小桶者在拎大桶者前面，容易求出出两人接满水等候（T+2t）分钟．可见，要使总的排队时间最短，拎小桶者应排在拎大桶者前面．这样，我们可以猜测，几个人拎着水桶在一个水龙头前面排队打水，要使总的排队时间最短，需将他们按水桶从小到大排队．
规律总结：
事实上，只要不按从小到大的顺序排队，就至少有紧挨着的两个人拎着大桶者排在拎小桶者之前，仍设大桶接满水需要T分钟，小桶接满水需要t分钟，并设拎大桶者开始接水时已等候了m分钟，这样拎大桶者接满水一共等候了（m+T）分钟，拎小桶者一共等候了（m+T+t）分钟，两人一共等候了（2m+2T+t）分钟，在其他人位置不变的前提下，让这两个人交还位置，即局部调整这两个人的位置，同样介意计算两个人接满水共等候了
2m+2t+T
2m+2t+T
分钟，共节省了
T-t
T-t
分钟，而其他人等候的时间未变，这说明只要存在有紧挨着的两个人是拎大桶者在拎小桶者之前都可以这样调整，从而使得总等候时间减少．这样经过一系列调整后，整个队伍都是从小打到排列，就打到最优状态，总的排队时间就最短．
【方法探究】
一般的，对某些设计多个可变对象的数学问题，先对其少数对象进行调整，其他对象暂时保持不变，从而化难为易，取得问题的局部解决．经过若干次这种局部的调整，不断缩小范围，逐步逼近目标，最终使问题得到解决，这种数学思想就叫做局部调整法．
【实践应用1】
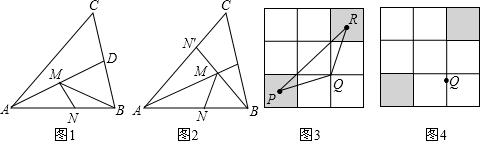
如图1在锐角△ABC中，AB=
4，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是多少？
解析：
（1）先假定N为定点，调整M到合适的位置使BM+MN有最小值（相对的），容易想到，在AC上作AN′=AN（即作点N关于AD的对称点N'），连接BN′交AD于M，则M点是使BM+MN有相对最小值的点．（如图2，M点是确定方法找到的）
（2）在考虑点N的位置，使BM+MN最终达到最小值．可以理解，BM+MN=BM+MN′，所以要使BM+MN′有最小值，只需使
BM+MN′=BN′
BM+MN′=BN′
，此时BM+MN的最小值是
4
4
．
【实践应用2】
如图3，把边长是3的正方形等分成9个小正方形，在有阴影的小正方形内（包括边界）分别取点P、R，于已知格点Q（每个小正方形的顶点叫做格点）构成三角形，则△PQR的最大面积是
2
2
，请在图4中画出面积最大时的△PQR的图形．
的点之间有无数多个点表示无理数；（6）（-6）2的平方根是-6；（7）-5是-25的平方根；（8）
是分数．其中正确的说法的个数是
