
科目:初中数学 来源: 题型:
 (2013•高淳县一模)某校九年级(1)班学生进行了一周的体育毕业考试训练,下面是该班学生训练前后的测试成绩统计图表(其中,统计图不完整).训练前成绩统计表.
(2013•高淳县一模)某校九年级(1)班学生进行了一周的体育毕业考试训练,下面是该班学生训练前后的测试成绩统计图表(其中,统计图不完整).训练前成绩统计表.
| 测试前 | 18~20分 | 21~23分 | 24~26分 | 27~29分 | 30分 |
| 人数 | 6 | 8 | 9 | 8 | 5 |
科目:初中数学 来源: 题型:阅读理解
| 2 |
科目:初中数学 来源:2011年上海市黄浦区中考数学二模试卷(解析版) 题型:解答题
| 成绩 | 461以下 | 461 到 470 | 471 到 480 | 481 到 490 | 491 到 500 | 501 到 510 | 511 到 520 | 521 到 530 | 531 到 540 | 541 到 550 | 551 到 560 | 561 到 570 | 571 到 580 | 580以上 | 合计 |
| 人数 | 628 | 88 | 110 | 98 | 120 | 135 | 215 | 236 | 357 | 380 | 423 | 356 | 126 | 28 | 3300 |
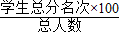 所得结果的整数部分(总分名次是按高到低排序),如学生甲的总分名次是356名,由
所得结果的整数部分(总分名次是按高到低排序),如学生甲的总分名次是356名,由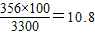 ,则他的定位分是10.如果该区小杰同学的定位分是38,那么他在区内的总分名次n的范围是______;
,则他的定位分是10.如果该区小杰同学的定位分是38,那么他在区内的总分名次n的范围是______;
科目:初中数学 来源: 题型:
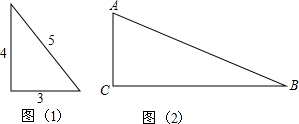
科目:初中数学 来源: 题型:解答题
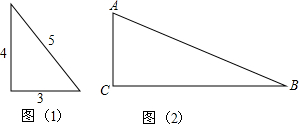
科目:初中数学 来源: 题型:
| 1 | 11 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com