
设a是一个负数,则数轴上表示数-a的点在( )
|
科目:初中数学 来源:2013年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
如图,已知抛物线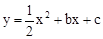 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
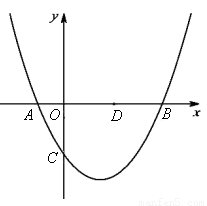
(1)b= ,点B的横坐标为 (上述结果均用含c的代数式表示);
(2)连接BC,过点A作直线AE∥BC,与抛物线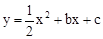 交于点E.点D是x轴上一点,其坐标为
交于点E.点D是x轴上一点,其坐标为
(2,0),当C,D,E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连接PB,PC,设所得△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有 个.
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(1)b= ,点B的横坐标为 (上述结果均用含c的代数式表示);
(2)连接BC,过点A作直线AE∥BC,与抛物线 交于点E.点D是x轴上一点,其坐标为
交于点E.点D是x轴上一点,其坐标为
(2,0),当C,D,E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连接PB,PC,设所得△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有 个.
科目:初中数学 来源:不详 题型:解答题
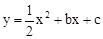 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).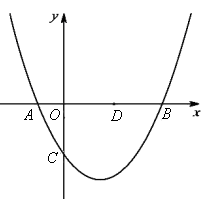
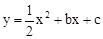 交于点E.点D是x轴上一点,其坐标为
交于点E.点D是x轴上一点,其坐标为科目:初中数学 来源: 题型:解答题
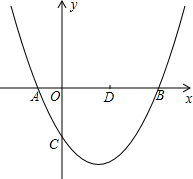 如图,已知抛物线y=
如图,已知抛物线y= x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0). x2+bx+c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;
x2+bx+c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com