
| 对于有理数a、b,有以下几种说法,其中正确的说法个数是( ) ①若a+b=0,则a与b互为相反数;②若a+b<0,则a与b异号;③a+b>0,则a与b同号时,则a>0,b>0;④|a|>|b|且a、b异号,则a+b>0;⑤|a|<b,则a+b>0.
|
科目:初中数学 来源: 题型:
科目:初中数学 来源:不详 题型:单选题
| A.3个 | B.2个 | C.1个 | D.0个 |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源:新教材新学案数学九年级上册 题型:044
上课时老师提出一个问题:如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌,

问:两张牌的牌面数字之和为几的概率最大?最大概率是多少?
小明、小颖、小亮三名同学分别进行了如下的求解过程.

小明的做法:
我借助于树状图,从树状图可以发现:总共有9种情况,每种情况发生的可能性相同,而两张牌的牌面数字和等于4的情况出现得最多,共3次,因此牌面数字和等于4的概率最大,概率为![]() ,即
,即![]() .
.
小颖的做法:
我通过列下表得到牌面数字之和等于4的概率最大,概率为![]() .
.

小亮的做法:
我也用了列表的方法,可我得到牌面数字之和等于4的概率为![]() .
.

你认为谁做得对?请说说你的理由.
科目:初中数学 来源: 题型:阅读理解
| 2 |
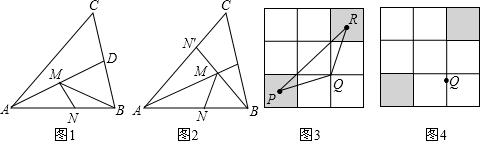
科目:初中数学 来源: 题型:阅读理解

科目:初中数学 来源:2012年山东省青岛市李沧区中考数学一模试卷(解析版) 题型:解答题
 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?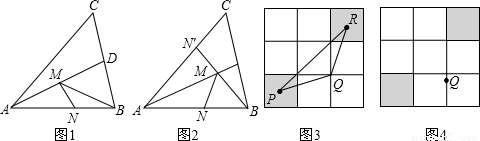
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com