
用代数式表示a,b两数的立方和与a,b两数的平方差的商是( )
|
科目:初中数学 来源: 题型:
| A、(a3+b3)÷(a2+b2) | ||
| B、a3+b3÷a2-b2 | ||
C、a3+
| ||
D、
|
科目:初中数学 来源:不详 题型:单选题
| A.(a3+b3)÷(a2+b2) | B.a3+b3÷a2-b2 | ||||
C.a3+
| D.
|
科目:初中数学 来源:双色笔记七年级数学(上)(北京师大版课标本) 题型:022
设甲数为x,乙数为y,用代数式表示:(注意除和除以的差别)
(1)甲、乙两数的差除以这两数的积:________;
(2)甲数的立方与乙数的4倍的差:________;
(3)甲数除乙数的商与乙数平方的差:________;
(4)甲数与乙数的立方差的一半:________.
科目:初中数学 来源:江苏省泰兴市黄桥区2012届九年级中考一模数学试题 题型:044
据悉,某市发改委拟于今年4月27日举行居民用水价格调整听证会,届时将有两个方案提供听证.如图(1),射线OA、射线OB分别表示现行的、方案一的每户每月的用水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;方案二如图(2)表格所示,每月的每立方米用水价格由该月的用水量决定,且第一、二、三级的用水价格之比为1∶1.5∶2(精确到0.01元后).
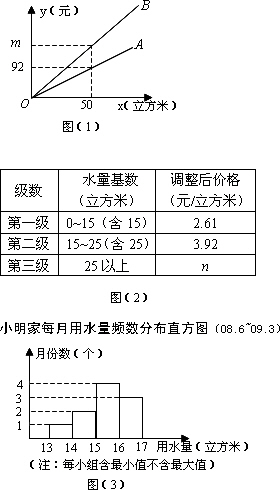
(1)写出现行的用水价是每立方米多少元?
(2)求图(1)中m的值和射线OB所对应的函数解析式,并写出定义域;
(3)若小明家某月的用水量是a立方米,请分别写出三种情况下(现行的、方案一和方案二)该月的水费b(用a的代数式表示);
(4)小明家最近10个月来的每月用水量的频数分布直方图
如图(3)所示,估计小明会赞同采用哪个方案?请说明理由.
科目:初中数学 来源: 题型:解答题
为了激发学生学习英语的兴趣,某中学举行了校园英文歌曲大赛,并设立了一、二、三等奖。学校计划根据设奖情况共买50件奖品,其中购买二等奖奖品件数比一等奖奖品件数的2倍件数还少10件,购买三等奖奖品所花钱数不超过二等奖所花钱数的1.5倍,且三等奖奖品数不能少于前两种奖品数之和.其中各种奖品的单价如下表所示,如果计划一等奖奖品买x件,买50件奖品的总费用是w元.
(1)用含有x的代数式表示:该校团委购买二等奖奖品多少件,三等奖奖品多少件?并表示w与x的函数关系式;
(2)请问共有哪几种方案?
(3)请你计算一下,学校应如何购买这三种奖品,才能使所支出的总费用最少,最少是多少元?
科目:初中数学 来源:不详 题型:解答题

科目:初中数学 来源: 题型:
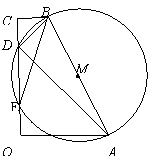
已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M交OC于D.E,连结AD、BD、BE。
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形。
_____________________,______________________ 。
(2)直角梯形OABC中,以O为坐标原点,A在x轴正半轴上建立直角坐标系(如图2),若抛物线![]() 经过点A.B.D,且B为抛物线的顶点。
经过点A.B.D,且B为抛物线的顶点。
①写出顶点B的坐标(用a的代数式表示)___________。
②求抛物线的解析式。
③在x轴下方的抛物线上是否存在这样的点P:过点P做PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标;若不存在,说明理由。
 | |||
 | |||
科目:初中数学 来源: 题型:
已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M交OC于D.E,连结AD、BD、BE。
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形。
_____________________,______________________ 。
(2)直角梯形OABC中,以O为坐标原点,A在x轴正半轴上建立直角坐标系(如图2),若抛物线![]() 经过点A.B.D,且B为抛物线的顶点。
经过点A.B.D,且B为抛物线的顶点。
①写出顶点B的坐标(用a的代数式表示)___________。
②求抛物线的解析式。
③在x轴下方的抛物线上是否存在这样的点P:过点P做PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标;若不存在,说明理由。
 | |||
 | |||
科目:初中数学 来源: 题型:
已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M交OC于D.E,连结AD、BD、BE。
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形。
_____________________,________________![]() ______ 。
______ 。
(2)直角梯形OABC中,以O为坐标原点,A在x轴正半轴上建立直角坐标系(如图2),若抛物线![]() 经过点A.B.D,且B为抛物线的顶点。
经过点A.B.D,且B为抛物线的顶点。
①写出顶点B的坐标(用a的代数式表示)___________。
②求抛物线的解析式。
③在x轴下方的抛物线上是否存在这样的![]() 点P:过点P做PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标;若不存在,说明理由。
点P:过点P做PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标;若不存在,说明理由。

|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com