已知关于x的不等式(2m-n)x>0,其中n>2m,则它的解集是( )| A.x>1 | B.x<0 | C.x>2m-n | D.x<2m-n |
|
相关习题
科目:初中数学
来源:
题型:
已知关于x的方程mx
2+(3-2m)x+(m-3)=0,其中m>0.
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2,其中x
1>x
2,若
y=,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围.
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
 已知关于x的方程mx2+(3-2m)x+(m-3)=0,其中m>0.
已知关于x的方程mx2+(3-2m)x+(m-3)=0,其中m>0.
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2,其中x1>x2,若 ,求y与m的函数关系式;
,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围.
查看答案和解析>>
科目:初中数学
来源:模拟题
题型:解答题
已知关于x的方程mx
2+(3-2m)x+(m-3)=0,其中m>0。
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2,其中x
1>x
2,若
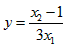
,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围。
查看答案和解析>>
科目:初中数学
来源:2011-2012学年北京市五十五中九年级(上)第一次月考数学试卷(解析版)
题型:解答题
已知关于x的方程mx
2+(3-2m)x+(m-3)=0,其中m>0.
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2,其中x
1>x
2,若

,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围.
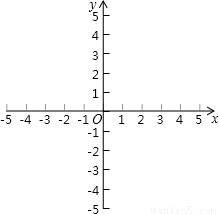
查看答案和解析>>
科目:初中数学
来源:2012年四川省成都市重点学校五校联考初三数学试卷(二)(解析版)
题型:解答题
已知关于x的方程mx
2+(3-2m)x+(m-3)=0,其中m>0.
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2,其中x
1>x
2,若

,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围.

查看答案和解析>>
科目:初中数学
来源:2012年四川省成都市青羊区中考数学一模试卷(解析版)
题型:解答题
已知关于x的方程mx
2+(3-2m)x+(m-3)=0,其中m>0.
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2,其中x
1>x
2,若

,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围.

查看答案和解析>>
科目:初中数学
来源:2012年浙江省杭州市中考数学模拟试卷(36)(解析版)
题型:解答题
已知关于x的方程mx
2+(3-2m)x+(m-3)=0,其中m>0.
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2,其中x
1>x
2,若

,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围.

查看答案和解析>>
科目:初中数学
来源:2011年河北省沧州市运河区中考数学二模试卷(解析版)
题型:解答题
已知关于x的方程mx
2+(3-2m)x+(m-3)=0,其中m>0.
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2,其中x
1>x
2,若

,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围.

查看答案和解析>>
科目:初中数学
来源:2011年北京市海淀区中考数学二模试卷 (解析版)
题型:解答题
已知关于x的方程mx
2+(3-2m)x+(m-3)=0,其中m>0.
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2,其中x
1>x
2,若
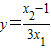
,求y与m的函数关系式;
(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤-m成立的m的取值范围.

查看答案和解析>>
科目:初中数学
来源:
题型:
已知:关于x的一元二次方程mx
2-(3m+2)x+2m+2=0(m>0).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2(其中x
1<x
2).若y是关于m的函数,且y=x
2-2x
1,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图象回答:当自变量m的取值范围满足什么条件时,y≤2m.
查看答案和解析>>

 已知关于x的方程mx2+(3-2m)x+(m-3)=0,其中m>0.
已知关于x的方程mx2+(3-2m)x+(m-3)=0,其中m>0. 已知关于x的方程mx2+(3-2m)x+(m-3)=0,其中m>0.
已知关于x的方程mx2+(3-2m)x+(m-3)=0,其中m>0. ,求y与m的函数关系式;
,求y与m的函数关系式;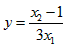 ,求y与m的函数关系式;
,求y与m的函数关系式;
 ,求y与m的函数关系式;
,求y与m的函数关系式;
 ,求y与m的函数关系式;
,求y与m的函数关系式;
 ,求y与m的函数关系式;
,求y与m的函数关系式;
 ,求y与m的函数关系式;
,求y与m的函数关系式;
 ,求y与m的函数关系式;
,求y与m的函数关系式;
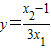 ,求y与m的函数关系式;
,求y与m的函数关系式;
 已知:关于x的一元二次方程mx2-(3m+2)x+2m+2=0(m>0).
已知:关于x的一元二次方程mx2-(3m+2)x+2m+2=0(m>0).