设某数为x，“比某数的

3

5

大1的数是4”，可列方程为（　　）

A．x[ 3 5 +(-1)]=4

B． 3 5 (x-1)=4

C． 3 5 x+1=4

D． 3 5 x-1=4

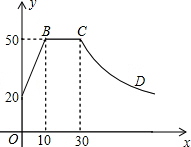心理学研究发现，一般情况下，在一节45分钟的课中，学生的活动随学习时间的变化而变化，开始学习时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生注意力开始分散，经过实验分析可知，学生的注意力指标数），随时间x（分钟）的变化规律如下图所示（其中AB、BC为线段，CD为双曲线的一部分）．
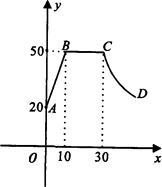
（1）分别求出当x≤10，10＜x＜30，以及x≥30时，注意力指标数y与时间x（分钟）之间的函数关系式；
（2）开始学习后第5分钟时与第35分钟时相比较，何时学生的注意力更集中？
（3）某数学内容的课堂学习大致可分为三个环节：即“教师引导，回顾旧知；自主探索，合作交流；总结归纳，巩固提高．”其中重点环节“自主探索，合作交流”这一过程需要30分钟才能完成，为了确保效果，要求学习时的注意力指标数不低于40．请问这样的课堂学习设计安排是否合理？并说明理由．

为了抓住“两会”商机，某商店决定购进甲、乙两种“两会”纪念品．若每个甲种纪念品的进价比每个乙种纪念品的进价少5元，且用80元购进甲种纪念品的数量与用100元购进乙种纪念品的数量相同．
（1）求每个甲种纪念品、每个乙种纪念品的进价分别为多少元？
（2）若该商店本次购进甲种纪念品的数量比购进乙种纪念品的数量的3倍还少5个，购进两种纪念品的总数量不超过95个，该商店每个甲种纪念品的销售价格为28元，每个乙种纪念品的销售价格为35元，则将本次购进的甲、乙两种纪念品全部售出后，可使销售两种纪念品的总利润（利润=售价-进价）超过740元，通过计算求出商店本次购进甲、乙两种纪念品有几种方案？请你设计出来．并求出最大的总利润是多少元？

为了抓住“两会”商机，某商店决定购进甲、乙两种“两会”纪念品．若每个甲种纪念品的进价比每个乙种纪念品的进价少5元，且用80元购进甲种纪念品的数量与用100元购进乙种纪念品的数量相同．
（1）求每个甲种纪念品、每个乙种纪念品的进价分别为多少元？
（2）若该商店本次购进甲种纪念品的数量比购进乙种纪念品的数量的3倍还少5个，购进两种纪念品的总数量不超过95个，该商店每个甲种纪念品的销售价格为28元，每个乙种纪念品的销售价格为35元，则将本次购进的甲、乙两种纪念品全部售出后，可使销售两种纪念品的总利润（利润=售价-进价）超过740元，通过计算求出商店本次购进甲、乙两种纪念品有几种方案？请你设计出来．并求出最大的总利润是多少元？

钢材是一种不会燃烧的建筑材料，它具有抗震，抗弯等特性．在实际应用中，钢材可以相对增加建筑物的荷载能力，满足建筑设计美感造型的需要，避免混凝土等建筑材料不能弯曲，拉伸的缺陷，因此钢材受到了建筑行业的青睐．重庆某钢材有限公司在去年3月至6月份销售甲、乙两种型号的钢材，已知甲种钢材每个月的售价y₁（百元/吨）与月份x之间的关系可用下表表示：

时间x（月）	3	4	5	6
售价y1（百元/吨）	72	54	43.2	36

甲种钢材的进价为30百元/吨，甲种钢材的销量P与月份x的关系式为P=300x；乙种钢材每个月的售价y₂（百元/吨）与月份x之间的关系满足二次函数y₂=ax²+x+c，已知乙种钢材的售价从3月的56百元/吨降至4月的53.5百元/吨，乙种钢材的进价为35百元/吨，乙种钢材3至6月平均每月的销量为1600吨．
（1）请观察题中的表格，用我们所学过的一次函数、反比例函数或者二次函数写出y₁与x之间的函数关系式；并求出y₂与x的函数关系式；
（2）已知该公司每个月在销售钢材时每吨需支出2百元的物流费用，问该公司销售甲、乙两种钢材哪个月获得的总利润最大，最大利润是多少百元？
（3）在去年7月至今年3月这9个月中，若每个月需固定支出甲、乙两种钢材的仓储成本各600百元，甲、乙两种钢材的进价每吨均比去年6月上涨1百元，每吨支出的物流费用变为2.5百元．该公司将甲、乙两种钢材的售价均在去年6月的基础上提高了p%，与此同时甲种钢材每月的销售量均在去年6月的基础上减少了0.5p%，乙种钢材每月的销售量均为1500吨，这样一来，该公司完成了去年7月至今年3月总利润459000百元的销售任务，请你参考以下数据，估算出p的值（精确到0.1）．（ 92.1²=8482.41，92.2²=8500.84，92.3²=8519.29，92.4²=8537.79）

钢材是一种不会燃烧的建筑材料，它具有抗震，抗弯等特性。在实际应用中，钢材可以相对增加建筑物的荷载能力，满足建筑设计美感造型的需要，避免混凝土等建筑材料不能弯曲，拉伸的缺陷，因此钢材受到了建筑行业的青睐。重庆某钢材有限公司在去年3月至6月份销售甲、乙两种型号的钢材，已知甲种钢材每个月的售价y₁（(百元/吨)）与月份x之间的关系可用下表表示：