
若线段AB、AC的长分别是一元二次方程x2-3x+2=0的两根,且A、B、C三点共线,则分别以线段AB、AC为直径的两圆的位置关系为( )
|
科目:初中数学 来源:不详 题型:单选题
| A.内切 | B.外切 | C.内含 | D.内切或外切 |
科目:初中数学 来源:2008-2009学年山东省济宁市泗水县九年级(上)段考数学试卷(21-24章)(解析版) 题型:选择题
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 7 |
| 4 |
科目:初中数学 来源: 题型:解答题
 )2+
)2+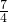 =0的两个根.
=0的两个根.科目:初中数学 来源:哈尔滨 题型:解答题
| 1 |
| 2 |
| 7 |
| 4 |
科目:初中数学 来源:新课标九年级数学竞赛培训第03讲:韦达定理(解析版) 题型:解答题
 )2+
)2+ =0的两个根.
=0的两个根.科目:初中数学 来源:2003年全国中考数学试题汇编《锐角三角函数》(03)(解析版) 题型:解答题
 )2+
)2+ =0的两个根.
=0的两个根.科目:初中数学 来源:2003年全国中考数学试题汇编《四边形》(04)(解析版) 题型:解答题
 )2+
)2+ =0的两个根.
=0的两个根.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com