
| 设a,b,c分别是△ABC的三个角A,B,C所对的边,研究A=2B是a2=b(b+c)的什么条件?以下是某同学的解法: 由A=2B,得sinA=sin2B,即:sinA=2sinB?cosB?a=2bcosB ?a=2b?
=b(b+c)(c-b) 所以,b=c或a2=b(b+c) 由此可知:A=2B是a2=b(b+c)的必要非充分条件. 请你研究这位同学解法的正误,并结合自己的思考,可以得到“A=2B”是“a2=b(b+c)”的( )条件.
|
科目:高中数学 来源: 题型:单选题
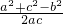 .变形得a2c=a2b+bc2-b3?a2(c-b)
.变形得a2c=a2b+bc2-b3?a2(c-b)科目:高中数学 来源:2010-2011学年浙江省杭州市萧山区三校联考高三(上)期中数学试卷(理科)(解析版) 题型:选择题
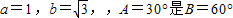 的( )
的( )科目:高中数学 来源: 题型:单选题
科目:高中数学 来源:新课标高三数学三角函数的图象正、余弦定理专项训练(河北) 题型:单选题
设a、b、c分别是△ABC的三个内角A、B、C所对的边,则a2=b是A=2B的( )
A.充要条件 B.充分而不必要条件
C.必要而充分条件 D.既不充分又不必要条件
科目:高中数学 来源:全优设计选修数学-1-1苏教版 苏教版 题型:013
设a、b、c分别是△ABC的三个内角A、B、C所对的边,则a2=b(b+c)是A=2B的
A.充要条件
B.充分而不必要条件
C.必要而不充分条件
D.既不充分又不必要条件
科目:高中数学 来源:江西省南昌市2008-2009学年度高三调研考试模拟训练理科数学 题型:044
设a,b,c分别是△ABC三个内角∠A,∠B,∠C的对边,若向量![]() ,
,
(1)求tanA·tanB的值;
(2)求![]() 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com