
若ab=2(a≠b),则两圆(x-a)2+y2=1和x2+(y-b)2=1的位置关系是( )
|
科目:高中数学 来源:2012-2013学年辽宁省大连市金州高级中学高二(上)10月月考数学试卷(理科)(解析版) 题型:选择题
科目:高中数学 来源: 题型:
 (A)选修4-1:几何证明选讲
(A)选修4-1:几何证明选讲| 13 |
| 13 |
|
科目:高中数学 来源:2009-2010学年浙江省温州中学高三(上)期中数学试卷(理科)(解析版) 题型:填空题
 +
+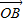 =
= ,则|AB|= .
,则|AB|= .科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
 轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.| x2 |
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
科目:高中数学 来源: 题型:
| x2 |
| 3 |
| |AB| |
| |FM| |
| 3 |
| X2 |
| 25 |
| Y2 |
| 9 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com