命题“?x∈R,x2-2x+2≤0”的否定为( )| A.?x∈R,x2-2x+2>0 | B.?x∈R,x2-2x+2≥0 | | C.?x∈R,x2-2x+2≤0 | D.?x∈R,x2-2x+2≥0 |
|
相关习题
科目:高中数学
来源:2012-2013学年湖南省郴州一中高二(上)期中数学试卷(理科)(解析版)
题型:选择题
命题“?x∈R,x2-2x+2≤0”的否定为( )
A.?x∈R,x2-2x+2>0
B.?x∈R,x2-2x+2≥0
C.?x∈R,x2-2x+2≤0
D.?x∈R,x2-2x+2≥0
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖南省郴州一中高二(上)期中数学试卷(理科)(解析版)
题型:选择题
命题“?x∈R,x2-2x+2≤0”的否定为( )
A.?x∈R,x2-2x+2>0
B.?x∈R,x2-2x+2≥0
C.?x∈R,x2-2x+2≤0
D.?x∈R,x2-2x+2≥0
查看答案和解析>>
科目:高中数学
来源:2010年吉林省延边州图们二高中高考数学模拟训练试卷1(文科)(解析版)
题型:选择题
命题“?x∈R,x2-2x+2≤0”的否定为( )
A.?x∈R,x2-2x+2>0
B.?x∈R,x2-2x+2≥0
C.?x∈R,x2-2x+2≤0
D.?x∈R,x2-2x+2≥0
查看答案和解析>>
科目:高中数学
来源:
题型:
命题“?x∈R,x2-2x+2≤0”的否定为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
命题“?x∈R,x
2-2x+2≤0”的否定为( )
| A.?x∈R,x2-2x+2>0 | B.?x∈R,x2-2x+2≥0 |
| C.?x∈R,x2-2x+2≤0 | D.?x∈R,x2-2x+2≥0 |
查看答案和解析>>
科目:高中数学
来源:
题型:
下列结论:①命题“?x∈R,x
2-x>0”的否定是“?x∈R,x
2-x≤0”;
②当x∈(1,+∞)时,函数
y=x,y=x2的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx
2-2x在区间(2,+∞)内是增函数,则实数m的取值范围为
m ≥ .
其中,正确结论的个数是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
下列结论:①命题“?x∈R,x
2-x>0”的否定是“?x∈R,x
2-x≤0”;
②当x∈(1,+∞)时,函数
y=x,y=x2的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx
2-2x在区间(2+∞)内是增函数,则实数m的取值范围为
m ≥ .
其中,正确结论的个数是( )
查看答案和解析>>
科目:高中数学
来源:2009年山东省滨州市高考数学一模试卷(文科)(解析版)
题型:选择题
下列结论:①命题“?x∈R,x
2-x>0”的否定是“?x∈R,x
2-x≤0”;
②当x∈(1,+∞)时,函数

的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx
2-2x在区间(2+∞)内是增函数,则实数m的取值范围为

.
其中,正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学
来源:2010年北京八中大兴分校高考数学模拟试卷(理科)(解析版)
题型:选择题
下列结论:①命题“?x∈R,x
2-x>0”的否定是“?x∈R,x
2-x≤0”;
②当x∈(1,+∞)时,函数

的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx
2-2x在区间(2+∞)内是增函数,则实数m的取值范围为
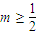
.
其中,正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
下列结论:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②当x∈(1,+∞)时,函数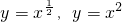 的图象都在直线y=x的上方;
的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx2-2x在区间(2+∞)内是增函数,则实数m的取值范围为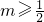 .
.
其中,正确结论的个数是
- A.
1
- B.
2
- C.
3
- D.
4
查看答案和解析>>

 的图象都在直线y=x的上方;
的图象都在直线y=x的上方; .
. 的图象都在直线y=x的上方;
的图象都在直线y=x的上方;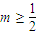 .
.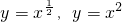 的图象都在直线y=x的上方;
的图象都在直线y=x的上方;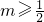 .
.