
| 以下命题正确的个数为( ) ①若a2+b2=8,则ab的最大值为4; ②若a>0,b>0,且a+b=4,则
③若x∈R,则x+
④若x>0,y>0,且4x+y=1,则xy的最大值为
|
科目:高中数学 来源:2009-2010学年宁夏银川一中高二(上)期中数学试卷(理科)(解析版) 题型:选择题
 的最小值为1;
的最小值为1;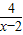 的最小值为6;
的最小值为6; .
.科目:高中数学 来源: 题型:
| 1 |
| a |
| 1 |
| b |
| 4 |
| x-2 |
| 1 |
| 4 |
科目:高中数学 来源:不详 题型:单选题
| 1 |
| a |
| 1 |
| b |
| 4 |
| x-2 |
| 1 |
| 4 |
| A.1 | B.2 | C.3 | D.4 |
科目:高中数学 来源:2011年《金版新学案》高三数学(文科)一轮复习测评卷:章末质量检测06(解析版) 题型:选择题
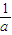 +
+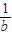 的最小值为1;
的最小值为1;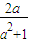 的最小值为1.
的最小值为1.科目:高中数学 来源: 题型:
| 1 |
| a |
| 1 |
| b |
| 2a |
| a2+1 |
| A、1 | B、2 | C、3 | D、4 |
科目:高中数学 来源:2008-2009学年浙江省温州市十校联合体高二(下)期末数学试卷(理科)(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源: 题型:
| 2 |
| a2+b2 |
| x2+y2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com