练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f（x）与g（x）满足：f（2+x）=f（2-x），g（x+1）=g（x-1），且f（x）在区间[2，+∞）上为减函数，令h（x）=f（x）?|g（x）|，则下列不等式正确的是（　　）
    A．.h（-2）≥h（4）B．h（-2）≤h（4）C．h（0）＞h（4）D．h（0）＜h（4）
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）与g（x）满足：f（2+x）=f（2-x），g（x+1）=g（x-1），且f（x）在区间[2，+∞）上为减函数，令h（x）=f（x）•|g（x）|，则下列不等式正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知函数f（x）与g（x）满足：f（2+x）=f（2-x），g（x+1）=g（x-1），且f（x）在区间[2，+∞）上为减函数，令h（x）=f（x）•|g（x）|，则下列不等式正确的是（　　）
    A．.h（-2）≥h（4）B．h（-2）≤h（4）C．h（0）＞h（4）D．h（0）＜h（4）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年辽宁省沈阳二中等重点中学协作体高考预测数学试卷08（理科）（解析版） 题型：选择题

    已知函数f（x）与g（x）满足：f（2+x）=f（2-x），g（x+1）=g（x-1），且f（x）在区间[2，+∞）上为减函数，令h（x）=f（x）•|g（x）|，则下列不等式正确的是（ ）
    A．.h（-2）≥h（4）
    B．h（-2）≤h（4）
    C．h（0）＞h（4）
    D．h（0）＜h（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知函数f（x）与g（x）满足：f（2+x）=f（2-x），g（x+1）=g（x-1），且f（x）在区间[2，+∞）上为减函数，令h（x）=f（x）•|g（x）|，则下列不等式正确的是


    1. A.
      .h（-2）≥h（4）
    2. B.
      h（-2）≤h（4）
    3. C.
      h（0）＞h（4）
    4. D.
      h（0）＜h（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

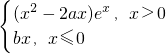    已知函数f（x）=数学公式，g（x）=clnx+b，且x=数学公式是函数y=f（x）的极值点．
    （Ⅰ）当b=-2时，求a的值，讨论函数f（x）的单调性；
    （Ⅱ）当b∈R时，函数y=f（x）-m有两个零点，求实数m的取值范围．
    （Ⅲ）是否存在这样的直线l，同时满足：
    ①l是函数y=f（x）的图象在点（2，f（2））处的切线
    ②l与函数y=g（x） 的图象相切于点P（x0，y0），x0∈[e-1，e]，如果存在，求实数b的取值范围；不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012年陕西省高考数学压轴卷（解析版） 题型：解答题

    定义：已知函数f（x）与g（x），若存在一条直线y=kx+b，使得对公共定义域内的任意实数均满足f（x）≤g（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx+b为曲线f（x）与g（x）的“左同旁切线”．已知f（x）=lnx，g（x）=1-．
    （1）试探求f（x）与g（x）是否存在“左同旁切线”，若存在，请求出左同旁切线方程；若不存在，请说明理由．
    （2）设P（x1，f（x1）），Q（x2，f（x2））是函数f（x）图象上任意两点，0＜x1＜x2，且存在实数x3＞0，使得f（x3）=，证明：x1＜x3＜x2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=2lnx-x2（x＞0）．
    （1）求函数f（x）的单调区间与最值；
    （2）若方程2xlnx+mx-x3=0在区间[
    1e
    ，e]    内有两个不相等的实根，求实数m的取值范围；  （其中e为自然对数的底数）
    （3）如果函数g（x）=f（x）-ax的图象与x轴交于两点A（x1，0），B（x2，0），且0＜x1＜x2，求证：g'（px1+qx2）＜0（其中，g'（x）是g（x）的导函数，正常数p，q满足p+q=1，q＞p）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=（x2-2ax）ex，g（x）=clnx+b，
    		2
    是函数y=f（x）的极值点，其中e是自然对数的底数．
    （Ⅰ）求实数a的值；
    （Ⅱ）直线l同时满足：
    ①l是函数y=f（x）的图象在点（2，f（2））处的切线；
    ②l与函数y=g（x）的图象相切于点P(x0，y0)，x0∈[e-1，e]．求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年广东省汕头市高二（下）质量监测数学试卷（文科）（解析版） 题型：解答题

    已知函数f（x）=ax2+bx+c（a≠0）满足：①f（0）=0；②?x∈R，f（x）≥x；③f（）=f（）．
    （1）求f（x）的表达式；
    （2）试讨论函数g（x）=f（x）-2x在区间[-2，2]内的单调性；
    （3）是否存在实数t，使得函数h（x）=f（x）-x2-x+t与函数u（x）=|log2x|（x∈（0，2]）的图象恒有两个不同交点，如果存在，求出相应t的取值范围；如果不存在，说明理由．

    查看答案和解析>>

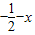    科目：高中数学 来源：2010-2011学年广东省惠州市惠阳高级中学高一（下）第二次段考数学试卷（解析版） 题型：解答题

    已知函数f（x）=ax2+ax和g（x）=x-a．其中a∈R且a≠0．
    （1）若函数f（x）与g（x）的图象的一个公共点恰好在x轴上，求a的值；
    （2）若p和q是方程f（x）-g（x）=0的两根，且满足，证明：当x∈（0，p）时，g（x）＜f（x）＜p-a．

    查看答案和解析>>


    同步练习册答案