已知数列{an}满足2an+1-an=0(n∈N*),则数列{an}一定是( )| A.公差为的等差数列 | B.公差为2的等差数列 | | C.公比为的等比数列 | D.公比为2的等比数列 |
|
相关习题
科目:高中数学
来源:花都区模拟
题型:单选题
已知数列{a
n}满足2a
n+1-a
n=0(n∈N
*),则数列{a
n}一定是( )
| A.公差为的等差数列 | B.公差为2的等差数列 |
| C.公比为的等比数列 | D.公比为2的等比数列 |
查看答案和解析>>
科目:高中数学
来源:2010-2011学年广东省广州市花都区高三调研数学试卷(理科)(解析版)
题型:选择题
已知数列{a
n}满足2a
n+1-a
n=0(n∈N
*),则数列{a
n}一定是( )
A.公差为

的等差数列
B.公差为2的等差数列
C.公比为

的等比数列
D.公比为2的等比数列
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}满足a
n+1=-a
n2+2a
n(n∈N
*),且0<a
1<1.
(1)用数学归纳法证明:0<a
n<1;
(2)若b
n=lg(1-a
n),且
a1=,求无穷数列
{}所有项的和.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知数列{an}满足an+1=-an2+2an(n∈N*),且0<a1<1.
(1)用数学归纳法证明:0<an<1;
(2)若bn=lg(1-an),且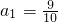 ,求无穷数列
,求无穷数列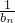 所有项的和.
所有项的和.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列{a
n}满足a
n+1=-a
n2+2a
n(n∈N
*),且0<a
1<1.
(1)用数学归纳法证明:0<a
n<1;
(2)若b
n=lg(1-a
n),且
a1=,求无穷数列
{}所有项的和.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年四川省南充高中高三(上)第二次月考数学试卷(理科)(解析版)
题型:解答题
已知数列{a
n}满足a
n+1=-a
n2+2a
n(n∈N
*),且0<a
1<1.
(1)用数学归纳法证明:0<a
n<1;
(2)若b
n=lg(1-a
n),且

,求无穷数列

所有项的和.
查看答案和解析>>
科目:高中数学
来源:2007-2008学年湖北省宜昌一中高三数学单元测试:数学归纳法、极限、导数(解析版)
题型:解答题
已知数列{a
n}满足a
n+1=-a
n2+2a
n(n∈N
*),且0<a
1<1.
(1)用数学归纳法证明:0<a
n<1;
(2)若b
n=lg(1-a
n),且

,求无穷数列
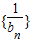
所有项的和.
查看答案和解析>>
科目:高中数学
来源:2008-2009学年湖北省宜昌一中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
已知数列{a
n}满足a
n+1=-a
n2+2a
n(n∈N
*),且0<a
1<1.
(1)用数学归纳法证明:0<a
n<1;
(2)若b
n=lg(1-a
n),且

,求无穷数列

所有项的和.
查看答案和解析>>
科目:高中数学
来源:2010年湖北省荆门市龙泉中学高三数学综合训练02(理科)(解析版)
题型:解答题
已知数列{a
n}满足a
n+1=-a
n2+2a
n(n∈N
*),且0<a
1<1.
(1)用数学归纳法证明:0<a
n<1;
(2)若b
n=lg(1-a
n),且

,求无穷数列

所有项的和.
查看答案和解析>>
科目:高中数学
来源:2011年四川省南充市南部中学高三段考数学试卷(理科)(解析版)
题型:解答题
已知数列{a
n}满足a
n+1=-a
n2+2a
n(n∈N
*),且0<a
1<1.
(1)用数学归纳法证明:0<a
n<1;
(2)若b
n=lg(1-a
n),且

,求无穷数列

所有项的和.
查看答案和解析>>

 的等差数列
的等差数列 的等比数列
的等比数列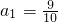 ,求无穷数列
,求无穷数列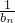 所有项的和.
所有项的和. ,求无穷数列
,求无穷数列 所有项的和.
所有项的和. ,求无穷数列
,求无穷数列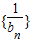 所有项的和.
所有项的和. ,求无穷数列
,求无穷数列 所有项的和.
所有项的和. ,求无穷数列
,求无穷数列 所有项的和.
所有项的和. ,求无穷数列
,求无穷数列 所有项的和.
所有项的和.