练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
     男女总计
    爱好402060
    不爱好203050
    总计6050110
    由k2=
    n(ad-bc)2
    (a+d)(c+d)(a+c)(b+d)
    算得，k2=
    110×(40×30-20×20)2
    60×50×60×50
    ≈7.8
    附表：
    p（k2≥k）0.0500.0100.001
    k3.8416.63510.828
    参照附表，得到的正确结论是（　　）
    A．有99%以上的把握认为“爱好该项运动与性别有关”
    B．有99%以上的把握认为“爱好该项运动与性别无关”
    C．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
    D．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别五关”
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
     男 女 总计
    爱好 40 20 60
    不爱好 20 30 50
    总计 60 50 110
    由k2=
    n(ad-bc)2
    (a+d)(c+d)(a+c)(b+d)
    算得，k2=
    110×(40×30-20×20)2
    60×50×60×50
    ≈7.8
    附表：
    p（k2≥k） 0.050 0.010 0.001
    k 3.841 6.635 10.828
    参照附表，得到的正确结论是（　　）
    A、有99%以上的把握认为“爱好该项运动与性别有关”
    B、有99%以上的把握认为“爱好该项运动与性别无关”
    C、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
    D、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别五关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
       男 女 总计
    爱好 40 20 60
    不爱好 20 30 50
    总计 60 50 110
    由k2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    算得，k2=
    110×(40×30-20×20)2
    60×50×60×50
    ≈7.8    ．
    P（K2≥k）  0.050 0.010 0.001
    k 3.841 6.635 10.828
    参照附表，得到的正确结论是（　　）
    A、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
    B、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”
    C、有99%以上的把握认为“爱好该项运动与性别有关”
    D、有99%以上的把握认为“爱好该项运动与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    通过随机询问110名性别不同的大学生是否爱好足球运动，得到如下的列联表：
    男 女 总计
    爱好 40 20 60
    不爱好 20 30 50
    总计 60 50 110
    （1）由分层抽样方法，抽取的55名学生爱好足球运动的应有几名？
    （2）运用2×2列联表进行独立性检验，参考下表你能得到什么统计学结论？
    P（K2≥k0） 0.100 0.050 0.025 0.010 0.001
    k0 2.706 3.841 5.024 6.635 10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    通过随机询问110名性别不同的大学生是否爱好某项运动，发现60名男生中有40人爱好这项运动，50名女生中有20人爱好这项运动，分析爱好此项运动是否与性别有关？有多大把握？
    P（k2≥k） 0.050 0.010 0.001
    k 3.841 6.635 10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
    男 女 总计
    爱好 40 20 60
    不爱好 20 30 50
    总计 60 50 110
    由K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    算得K2=
    110×(40×30-20×20)2
    60×50×60×50
    ≈7.8
    附表：
    P（K2≥k） 0.050 0.010 0.001
    k 3.841 6.635 10.828
    参照附表，得到的正确结论是
    ①③⑤
    ①③⑤
    ．
    ①在犯错误的概率不超过1%的前提下，认为“爱好该项运动与性别有关”．
    ②在犯错误的概率不超过1%的前提下，认为“爱好该项运动与性别无关”．
    ③在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关”．
    ④在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关”．
    ⑤有99%以上的把握认为“爱好该项运动与性别有关”．
    ⑥有99%以上的把握认为“爱好该项运动与性别无关”．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年上海交大附中高三数学理总复习二统计、统计案例练习卷（解析版） 题型：选择题

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：

     

    男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

    由K2＝算得，K2＝≈7.8.

    附表：

    P(K2≥k)

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是(　　)

    A．有99%以上的把握认为“爱好该项运动与性别有关”

    B．有99%以上的把握认为“爱好该项运动与性别无关”

    C．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”

    D．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”

     

    查看答案和解析>>

    科目：高中数学 来源：2014届陕西省高二下学期期中考试数学文试卷（解析版） 题型：选择题

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的

    列联表：

     

     男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

    由算得，

    附表： 

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是（  ）

    有99%以上的把握认为“爱好该项运动与性别有关”

    有99%以上的把握认为“爱好该项运动与性别无关”

    在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别有关”

    在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别无关”

     

    查看答案和解析>>

    科目：高中数学 来源：2014届广东省高二下学期期中文科数学试卷（解析版） 题型：选择题

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：

     

     男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

    由 算得，

    附表： 

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是 （   ）

    A．有99%以上的把握认为“爱好该项运动与性别有关”

    B．有99%以上的把握认为“爱好该项运动与性别无关”

    C．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别有关”

    D．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别无关”

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖南省五市十高三第一次合检测文科数学试卷（解析版） 题型：选择题

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：

     

     男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

    由 算得，

    附表： 

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是（    ）

    A．有99%以上的把握认为“爱好该项运动与性别有关”

    B．有99%以上的把握认为“爱好该项运动与性别无关”

    C．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别有关”

    D．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别无关”

     

    查看答案和解析>>

    科目：高中数学 来源：2013届黑龙江牡丹江一中高二下学期期末考试理科数学试卷（解析版） 题型：选择题

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列

    由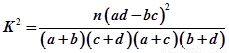算得，

    ．

    参照附表，得到的正确结论是 （   ）

    A、再犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别有关”

    B、再犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别无关”

    C、有99%以上的把握认为“爱好该项运动与性别有关”

    D、有99%以上的把握认为“爱好该项运动与性别无关”

     

    查看答案和解析>>


    同步练习册答案