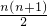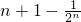| 设f(x),g(x)是定义在R上的恒不为零的函数,对任意x,y∈R,都有f(x)f(y)=f(x+y),g(x)+g(y)=g(x+y),若a1=,an=f(n)(n∈N*),且b1=1,bn=g(n)(n∈N*),则数列{anbn}的前n项和为Sn为( ) |
相关习题
科目:高中数学
来源:
题型:
设f(x),g(x)是定义在R上的恒大于零的可导函数,且满足f′(x)g(x)-f(x)g′(x)>0,则当a<x<b时有( )
| A、f(x)g(x)>f(b)g(b) | B、f(x)g(a)>f(a)g(x) | C、f(x)g(b)>f(b)g(x) | D、f(x)g(x)>f(a)g(a) |
查看答案和解析>>
科目:高中数学
来源:东城区一模
题型:单选题
设f(x),g(x)是定义在R上的恒大于零的可导函数,且满足f′(x)g(x)-f(x)g′(x)>0,则当a<x<b时有( )
| A.f(x)g(x)>f(b)g(b) | B.f(x)g(a)>f(a)g(x) | C.f(x)g(b)>f(b)g(x) | D.f(x)g(x)>f(a)g(a) |
查看答案和解析>>
科目:高中数学
来源:安徽模拟
题型:单选题
设f(x),g(x)是定义在R上的恒不为零的函数,对任意x,y∈R,都有f(x)f(y)=f(x+y),g(x)+g(y)=g(x+y),若
a1=,an=f(n)(n∈N*),且
b1=1,bn=g(n)(n∈N*),则数列{a
nb
n}的前n项和为S
n为( )
查看答案和解析>>
科目:高中数学
来源:2007-2008学年湖北省宜昌一中高三数学单元测试:数学归纳法、极限、导数(解析版)
题型:选择题
设f(x),g(x)是定义在R上的恒大于零的可导函数,且满足f′(x)g(x)-f(x)g′(x)>0,则当a<x<b时有( )
A.f(x)g(x)>f(b)g(b)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(b)>f(b)g(x)
D.f(x)g(x)>f(a)g(a)
查看答案和解析>>
科目:高中数学
来源:2010-2011学年浙江省宁波市鄞州高级中学高二(上)期末数学试卷(理科)(解析版)
题型:选择题
设f(x),g(x)是定义在R上的恒大于零的可导函数,且满足f′(x)g(x)-f(x)g′(x)>0,则当a<x<b时有( )
A.f(x)g(x)>f(b)g(b)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(b)>f(b)g(x)
D.f(x)g(x)>f(a)g(a)
查看答案和解析>>
科目:高中数学
来源:2010-2011学年福建省龙岩市永定一中高二(下)第一次段考数学试卷(理科)(解析版)
题型:选择题
设f(x),g(x)是定义在R上的恒大于零的可导函数,且满足f′(x)g(x)-f(x)g′(x)>0,则当a<x<b时有( )
A.f(x)g(x)>f(b)g(b)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(b)>f(b)g(x)
D.f(x)g(x)>f(a)g(a)
查看答案和解析>>
科目:高中数学
来源:2010年广东省茂名一中高考数学二模试卷(解析版)
题型:选择题
设f(x),g(x)是定义在R上的恒大于零的可导函数,且满足f′(x)g(x)-f(x)g′(x)>0,则当a<x<b时有( )
A.f(x)g(x)>f(b)g(b)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(b)>f(b)g(x)
D.f(x)g(x)>f(a)g(a)
查看答案和解析>>
科目:高中数学
来源:《数列》2013年广东省广州大学附中高考数学二轮复习检测(解析版)
题型:选择题
设f(x),g(x)是定义在R上的恒不为零的函数,对任意x,y∈R,都有f(x)f(y)=f(x+y),g(x)+g(y)=g(x+y),若

,且
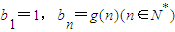
,则数列{a
nb
n}的前n项和为S
n为( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:2011-2012学年安徽省省城名校高三第四次联考数学试卷(理科)(解析版)
题型:选择题
设f(x),g(x)是定义在R上的恒不为零的函数,对任意x,y∈R,都有f(x)f(y)=f(x+y),g(x)+g(y)=g(x+y),若

,且

,则数列{a
nb
n}的前n项和为S
n为( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:
题型:单选题
设f(x),g(x)是定义在R上的恒不为零的函数,对任意x,y∈R,都有f(x)f(y)=f(x+y),g(x)+g(y)=g(x+y),若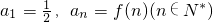 ,且
,且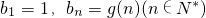 ,则数列{anbn}的前n项和为Sn为
,则数列{anbn}的前n项和为Sn为
- A.
- B.
- C.
- D.
查看答案和解析>>

 ,且
,且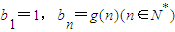 ,则数列{anbn}的前n项和为Sn为( )
,则数列{anbn}的前n项和为Sn为( )



 ,且
,且 ,则数列{anbn}的前n项和为Sn为( )
,则数列{anbn}的前n项和为Sn为( )



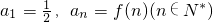 ,且
,且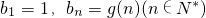 ,则数列{anbn}的前n项和为Sn为
,则数列{anbn}的前n项和为Sn为