
已知等差数列{an}满足:a1>0,a1+a2+a3+…+a101=0,则使前n项和sn取得最大值的n值为( )
|
科目:高中数学 来源:河池模拟 题型:单选题
| A.50 | B.51 | C.50或51 | D.51或52 |
科目:高中数学 来源:2013年广西河池市、柳州市、贵港市、钦州市高三1月模拟数学试卷(文科)(解析版) 题型:选择题
科目:高中数学 来源: 题型:
| 1 | 2 |
科目:高中数学 来源:2009-2010学年江苏省南京九中高三(上)期中数学练习试卷(文科)(解析版) 题型:解答题

 ,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.
,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.科目:高中数学 来源:《第2章 数列》2010年单元测试卷(3)(解析版) 题型:解答题

 ,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.
,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.科目:高中数学 来源:2009-2010学年江苏省徐州市高三(上)10月调研数学试卷(解析版) 题型:解答题
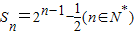
 ,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.
,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.科目:高中数学 来源:2010年江苏省南通市高考数学模拟试卷(二)(解析版) 题型:解答题

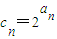 ,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.
,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.科目:高中数学 来源:高考数学复习练习卷(二)(解析版) 题型:解答题
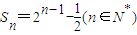
 ,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.
,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.科目:高中数学 来源:2011年江苏省重点中学高考数学一轮复习课时练精品:29-32(解析版) 题型:解答题

 ,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.
,试问:是否存在正整数n,使不等式bncn+1>bn+cn成立?若存在,求出相应n的值;若不存在,请说明理由.科目:高中数学 来源:广东省高要市新桥中学2013届高三12月月考数学(文)试题 题型:013
已知等差数列{an}满足a1+a2+a3+…+a101=0,则有:
A.a1+a101>0
B.a2+a100<0
C.a3+a99=0
D.a51=51
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com