
已知函数y=f(x),将f(x)的图象上的每一点的纵坐标保持不变,横坐标扩大到原来的2倍,然后把所得的图象沿着x轴向左平移
|
科目:高中数学 来源: 题型:
| π |
| 6 |
科目:高中数学 来源:肇庆一模 题型:单选题
| π |
| 2 |
| 1 |
| 2 |
A.f(x)=
| B.f(x)=
| ||||||||||
C.f(x)=
| D.f(x)=
|
科目:高中数学 来源:2012年广东省肇庆市高考数学一模试卷(文科)(解析版) 题型:选择题
 个单位,这样得到的是
个单位,这样得到的是 的图象,那么函数y=f(x)的解析式是( )
的图象,那么函数y=f(x)的解析式是( )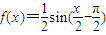

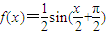

科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| 2 |
科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| 2 |
科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| 2 |
A、y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
科目:高中数学 来源:不详 题型:单选题
| π |
| 2 |
| 1 |
| 2 |
A.y=
| B.y=
| ||||||||||
C.y=
| D.y=
|
科目:高中数学 来源:2009-2010学年河北省衡水中学高一(上)三调数学试卷(解析版) 题型:选择题
 个单位,这样得到的曲线与
个单位,这样得到的曲线与 的图象相同,则y=f(x)的解析式是( )
的图象相同,则y=f(x)的解析式是( )



科目:高中数学 来源:2012-2013学年重庆市酉阳一中高三(上)第一次月考数学试卷(文科)(解析版) 题型:选择题
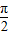 个单位,这样得到的曲线与
个单位,这样得到的曲线与 的图象相同,则y=f(x)的解析式是( )
的图象相同,则y=f(x)的解析式是( )



科目:高中数学 来源:2006年广东省广州市普通高中数学必修模块综合训练(一)(解析版) 题型:选择题
 个单位,这样得到的曲线与
个单位,这样得到的曲线与 的图象相同,则y=f(x)的解析式是( )
的图象相同,则y=f(x)的解析式是( )



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com