(理)设Sn是无穷等比数列的前n项和,若Sn=,则首项a1的取值范围是( )| A.(0,) | B.(0,) | C.(0,)∪(,) | D.(0,)∪(,0) |
|
相关习题
科目:高中数学
来源:
题型:
(理)设S
n是无穷等比数列的前n项和,若
S
n=
,则首项a
1的取值范围是( )
| A、(0,) |
| B、(0,) |
| C、(0,)∪(,) |
| D、(0,)∪(,0) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
(理)设S
n是无穷等比数列的前n项和,若
S
n=
,则首项a
1的取值范围是( )
| A.(0,) | B.(0,) | C.(0,)∪(,) | D.(0,)∪(,0) |
查看答案和解析>>
科目:高中数学
来源:2009-2010学年重庆市西南师大附中高三(上)9月月考数学试卷(理科)(解析版)
题型:选择题
(理)设S
n是无穷等比数列的前n项和,若
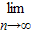
S
n=

,则首项a
1的取值范围是( )
A.(0,

)
B.(0,

)
C.(0,

)∪(
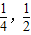
)
D.(0,

)∪(

,0)
查看答案和解析>>
科目:高中数学
来源:2007年天津市汉沽一中高三第一次调研数学试卷(解析版)
题型:选择题
(理)设S
n是无穷等比数列的前n项和,若
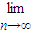
S
n=

,则首项a
1的取值范围是( )
A.(0,

)
B.(0,

)
C.(0,

)∪(
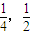
)
D.(0,

)∪(

,0)
查看答案和解析>>
科目:高中数学
来源:
题型:
已知公比为q(0<q<1)的无穷等比数列{a
n}各项的和为9,无穷等比数列{a
n2}各项的和为
.
(1)求数列{a
n}的首项a
1和公比q;
(2)对给定的k(k=1,2,3,…,n),设T
(k)是首项为a
k,公差为2a
k-1的等差数列,求T
(2)的前2007项之和;
(3)(理)设b
i为数列T
(i)的第i项,S
n=b
1+b
2+…+b
n:
①求S
n的表达式,并求出S
n取最大值时n的值.
②求正整数m(m>1),使得
存在且不等于零.
(文)设b
i为数列T
(i)的第i项,S
n=b
1+b
2+…+b
n:求S
n的表达式,并求正整数m(m>1),使得
存在且不等于零.
查看答案和解析>>
科目:高中数学
来源:广东
题型:解答题
已知公比为q(0<q<1)的无穷等比数列{a
n}各项的和为9,无穷等比数列{a
n2}各项的和为
.
(1)求数列{a
n}的首项a
1和公比q;
(2)对给定的k(k=1,2,3,…,n),设T
(k)是首项为a
k,公差为2a
k-1的等差数列,求T
(2)的前2007项之和;
(3)(理)设b
i为数列T
(i)的第i项,S
n=b
1+b
2+…+b
n:
①求S
n的表达式,并求出S
n取最大值时n的值.
②求正整数m(m>1),使得
存在且不等于零.
(文)设b
i为数列T
(i)的第i项,S
n=b
1+b
2+…+b
n:求S
n的表达式,并求正整数m(m>1),使得
存在且不等于零.
查看答案和解析>>
科目:高中数学
来源:2006年广东省高考数学试卷(解析版)
题型:解答题
已知公比为q(0<q<1)的无穷等比数列{a
n}各项的和为9,无穷等比数列{a
n2}各项的和为
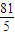
.
(1)求数列{a
n}的首项a
1和公比q;
(2)对给定的k(k=1,2,3,…,n),设T
(k)是首项为a
k,公差为2a
k-1的等差数列,求T
(2)的前2007项之和;
(3)(理)设b
i为数列T
(i)的第i项,S
n=b
1+b
2+…+b
n:
①求S
n的表达式,并求出S
n取最大值时n的值.
②求正整数m(m>1),使得
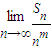
存在且不等于零.
(文)设b
i为数列T
(i)的第i项,S
n=b
1+b
2+…+b
n:求S
n的表达式,并求正整数m(m>1),使得
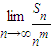
存在且不等于零.
查看答案和解析>>
科目:高中数学
来源:2009-2010年上海市华东师大二附中高三数学综合练习试卷(09)(解析版)
题型:解答题
已知公比为q(0<q<1)的无穷等比数列{a
n}各项的和为9,无穷等比数列{a
n2}各项的和为

.
(1)求数列{a
n}的首项a
1和公比q;
(2)对给定的k(k=1,2,3,…,n),设T
(k)是首项为a
k,公差为2a
k-1的等差数列,求T
(2)的前2007项之和;
(3)(理)设b
i为数列T
(i)的第i项,S
n=b
1+b
2+…+b
n:
①求S
n的表达式,并求出S
n取最大值时n的值.
②求正整数m(m>1),使得
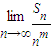
存在且不等于零.
(文)设b
i为数列T
(i)的第i项,S
n=b
1+b
2+…+b
n:求S
n的表达式,并求正整数m(m>1),使得

存在且不等于零.
查看答案和解析>>
科目:高中数学
来源:2008-2009学年上海市普陀区曹杨二中高三(上)入学摸底数学试卷(解析版)
题型:解答题
已知无穷数列{a
n}中,a
1,a
2,…,a
m是以10为首项,以-2为公差的等差数列;a
m+1,a
m+2,…,a
2m是以

为首项,以

为公比的等比数列(m≥3,m∈N
*);并且对一切正整数n,都有a
n+2m=a
n成立.
(1)当m=3时,请依次写出数列{a
n}的前12项;
(2)若a
23=-2,试求m的值;
(3)设数列{a
n}的前n项和为S
n,问是否存在m的值,使得S
128m+3≥2008成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:2008年上海市普陀区高考数学二模试卷(解析版)
题型:解答题
已知无穷数列{a
n}中,a
1,a
2,…,a
m是以10为首项,以-2为公差的等差数列;a
m+1,a
m+2,…,a
2m是以

为首项,以

为公比的等比数列(m≥3,m∈N
*);并且对一切正整数n,都有a
n+2m=a
n成立.
(1)当m=3时,请依次写出数列{a
n}的前12项;
(2)若a
23=-2,试求m的值;
(3)设数列{a
n}的前n项和为S
n,问是否存在m的值,使得S
128m+3≥2008成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>

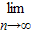 Sn=
Sn= ,则首项a1的取值范围是( )
,则首项a1的取值范围是( ) )
) )
) )∪(
)∪(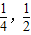 )
) )∪(
)∪( ,0)
,0)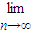 Sn=
Sn= ,则首项a1的取值范围是( )
,则首项a1的取值范围是( ) )
) )
) )∪(
)∪(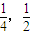 )
) )∪(
)∪( ,0)
,0)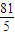 .
.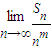 存在且不等于零.
存在且不等于零.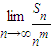 存在且不等于零.
存在且不等于零. .
.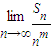 存在且不等于零.
存在且不等于零. 存在且不等于零.
存在且不等于零. 为首项,以
为首项,以 为公比的等比数列(m≥3,m∈N*);并且对一切正整数n,都有an+2m=an成立.
为公比的等比数列(m≥3,m∈N*);并且对一切正整数n,都有an+2m=an成立. 为首项,以
为首项,以 为公比的等比数列(m≥3,m∈N*);并且对一切正整数n,都有an+2m=an成立.
为公比的等比数列(m≥3,m∈N*);并且对一切正整数n,都有an+2m=an成立.