已知f(x)=x+x3,x1、x2、x3∈R,且x1+x2>0,x2+x3>0,x3+x1>0,则f(x1)+f(x2)+f(x3)的值( )| A.是正数 | | B.是负数 | | C.是零 | | D.可能是正数也可能是负数或是零 |
|
相关习题
科目:高中数学
来源:2008-2009学年湖北省百所重点中学高三第一次联考数学试卷(文科)(解析版)
题型:选择题
已知f(x)=x+x3,x1、x2、x3∈R,且x1+x2>0,x2+x3>0,x3+x1>0,则f(x1)+f(x2)+f(x3)的值( )
A.是正数
B.是负数
C.是零
D.可能是正数也可能是负数或是零
查看答案和解析>>
科目:高中数学
来源:湖北模拟
题型:单选题
已知f(x)=x+x
3,x
1、x
2、x
3∈R,且x
1+x
2>0,x
2+x
3>0,x
3+x
1>0,则f(x
1)+f(x
2)+f(x
3)的值( )
| A.是正数 |
| B.是负数 |
| C.是零 |
| D.可能是正数也可能是负数或是零 |
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知f(x)=x+x3,x1、x2、x3∈R,且x1+x2>0,x2+x3>0,x3+x1>0,则f(x1)+f(x2)+f(x3)的值
- A.
是正数
- B.
是负数
- C.
是零
- D.
可能是正数也可能是负数或是零
查看答案和解析>>
科目:高中数学
来源:
题型:
(2009•湖北模拟)已知f(x)=x+x3,x1、x2、x3∈R,且x1+x2>0,x2+x3>0,x3+x1>0,则f(x1)+f(x2)+f(x3)的值( )
查看答案和解析>>
科目:高中数学
来源:福建省高考真题
题型:解答题
已知f(x)=4x+ax
2-
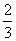
x
3(x∈R)在区间[-1,1]上是增函数,
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=2x+

x
3的两个非零实根为x
1、x
2,试问:是否存在实数m,使得不等式m
2+tm+1≥|x
1-x
2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学
来源:
题型:
已知定义在R上的奇函数f(x)=x3+bx2+cx+d在x=±1处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)试证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4成立;
(Ⅲ)若过点P(m,n),(m、n∈R,且|m|<2)可作曲线y=f(x)的三条切线,试求点P对应平面区域的面积.
查看答案和解析>>
科目:高中数学
来源:选修一综合试卷(2)(解析版)
题型:解答题
已知定义在R上的奇函数f(x)=x3+bx2+cx+d在x=±1处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)试证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4成立;
(Ⅲ)若过点P(m,n),(m、n∈R,且|m|<2)可作曲线y=f(x)的三条切线,试求点P对应平面区域的面积.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年北京市东城区东直门中学高三数学提高测试试卷3(理科)(解析版)
题型:解答题
已知定义在R上的奇函数f(x)=x3+bx2+cx+d在x=±1处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)试证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4成立;
(Ⅲ)若过点P(m,n),(m、n∈R,且|m|<2)可作曲线y=f(x)的三条切线,试求点P对应平面区域的面积.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年福建省永春一中、培元中学、季延中学、石狮联中高考数学一模试卷(文科)(解析版)
题型:解答题
已知定义在R上的奇函数f(x)=x3+bx2+cx+d在x=±1处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)试证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4成立;
(Ⅲ)若过点P(m,n),(m、n∈R,且|m|<2)可作曲线y=f(x)的三条切线,试求点P对应平面区域的面积.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年福建省四校高三第一次联考数学试卷(文科)(解析版)
题型:解答题
已知定义在R上的奇函数f(x)=x3+bx2+cx+d在x=±1处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)试证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4成立;
(Ⅲ)若过点P(m,n),(m、n∈R,且|m|<2)可作曲线y=f(x)的三条切线,试求点P对应平面区域的面积.
查看答案和解析>>

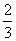 x3(x∈R)在区间[-1,1]上是增函数,
x3(x∈R)在区间[-1,1]上是增函数, x3的两个非零实根为x1、x2,试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。
x3的两个非零实根为x1、x2,试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。