
高三某班有60名学生(其中女生有20名),三好学生占
|
科目:高中数学 来源: 题型:
| 1 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
科目:高中数学 来源: 题型:
高三某班有60名学生(其中女生有20名),三好学生占![]() ,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
科目:高中数学 来源:黑龙江省2009-2010学年度上学期高三期末(数学理)试题 题型:选择题
高三某班有60名学生(其中女生有20名),三好学生占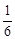 ,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
(A)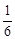 (B)
(B)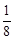 (C)
(C) (D)
(D)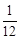
科目:高中数学 来源:不详 题型:单选题
| 1 |
| 6 |
A.
| B.
| C.
| D.
|
科目:高中数学 来源:2013年山东省高考数学预测试卷(06)(解析版) 题型:选择题
 ,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )

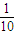
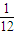
科目:高中数学 来源:2013年山东省高考数学预测试卷(05)(解析版) 题型:选择题
 ,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )


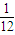
科目:高中数学 来源:2010年高考数学最有可能考的50题(解析版) 题型:选择题
 ,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )

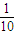

科目:高中数学 来源: 题型:单选题
 ,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是
,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是



科目:高中数学 来源:不详 题型:单选题
 ,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )
,而且三好学生中女生占一半,现在从该班任选一名学生参加座谈会,则在已知没有选上女生的条件下,选上的是三好学生的概率是( )A. | B. | C. | D. |
科目:高中数学 来源:不详 题型:解答题
| 编号 | 性别 | 投篮成绩 |
| 2 | 男 | 90 |
| 7 | 女 | 60 |
| 12 | 男 | 75 |
| 17 | 男 | 80 |
| 22 | 女 | 83 |
| 27 | 男 | 85 |
| 32 | 女 | 75 |
| 37 | 男 | 80 |
| 42 | 女 | 70 |
| 47 | 女 | 60 |
| 编号 | 性别 | 投篮成绩 |
| 1 | 男 | 95 |
| 8 | 男 | 85 |
| 10 | 男 | 85 |
| 20 | 男 | 70 |
| 23 | 男 | 70 |
| 28 | 男 | 80 |
| 33 | 女 | 60 |
| 35 | 女 | 65 |
| 43 | 女 | 70 |
| 48 | 女 | 60 |
| | 优秀 | 非优秀 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | 10 |
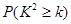 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
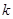 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com